Distancia focal de una elipse

A continuación, veremos ejemplos de cómo calcular la distancia focal paso a paso.

Cómo calcular la distancia focal

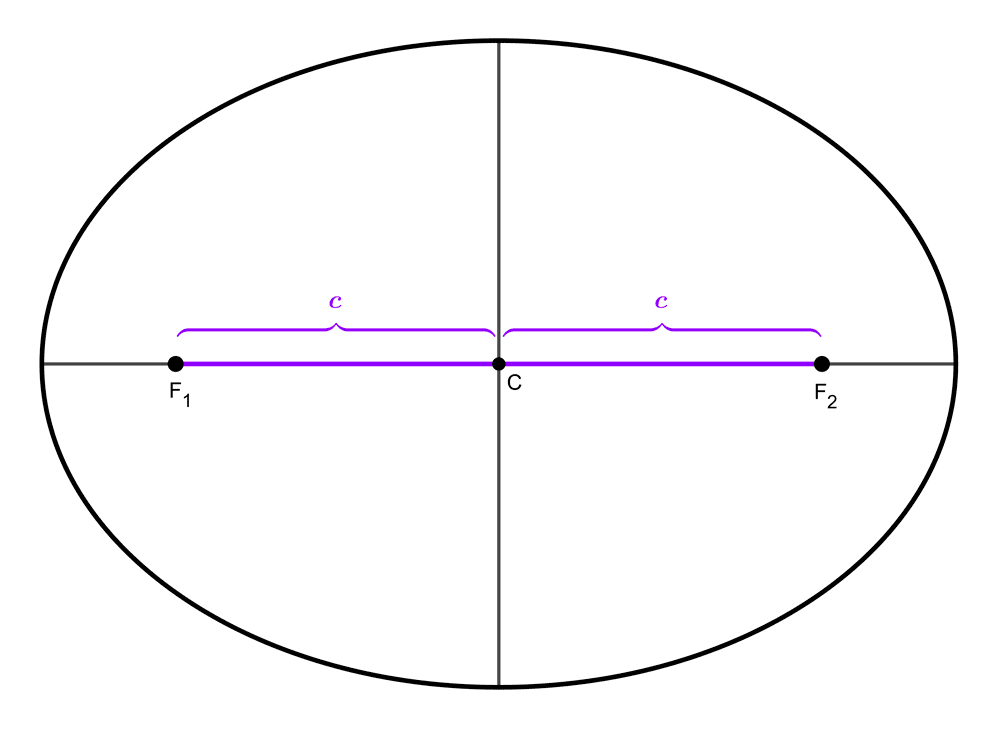
Como dijimos al principio, la semidistancia focal se relaciona con los valores de los semiejes a y b a través de la siguiente fórmula:

*c^2=a^2-b^2* de donde se deduce que *c=\sqrt{a^2-b^2}*

La última ecuación permite obtener el valor de c, para hallar la distancia focal basta con multiplicar c por 2. Otra forma es directamente usando la fórmula de la distancia focal: 

*2c=2\sqrt{a^2-b^2}*

Si se conocen los focos F₁(x₁, y₁) y F₂(x₂, y₂), puede usarse la fórmula de distancia entre dos puntos para hallar la distancia focal:

*2c=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}*

Ejercicios resueltos

A continuación resolvemos algunos ejercicios sobre el cálculo de la distancia focal.

Ejercicio 1

Calcular la distancia focal de la elipse *\dfrac{x^2}{4}+\dfrac{y^2}{25}=1*

Solución: el problema nos da una ecuación canónica de la cual se pueden extraer los cuadrados de los semiejes, que son los denominadores de las variables:

*a^2=25*

*b^2=4*

Con estos datos usamos la fórmula de la semidistancia focal:

*c=\sqrt{a^2-b^2}*

*c=\sqrt{25-4}*

*c=\sqrt{21}*

Ahora multiplicamos por dos para obtener la distancia focal:

*2c=2\cdot \sqrt{21}≈9,16*

Por tanto, la distancia focal de la elipse es *2\sqrt{21},* aproximadamente 9,16 unidades.

Ejercicio 2

Determinar cuál es la distancia focal de un elipse cuya longitud del eje mayor es 26 cm y la longitud de su eje menor es 24 cm.

Solución: el problema no nos da una ecuación pero sí las longitudes de los ejes, con lo cual se pueden obtener las medidas de los semiejes:

*2a=26→a=\dfrac{26}{2}=13*

*2b=24→b=\dfrac{24}{2}=12*

Con estos datos, calculamos la semidistancia focal usando la fórmula:

*c=\sqrt{a^2-b^2}*

*c=\sqrt{13^2-12^2}*

*c=\sqrt{169-144}*

*c=\sqrt{25}*

*c=5*

Hemos obtenido la mitad de la distancia focal, para sacar la medida completa multiplicamos por dos:

*2c=2\cdot 5=10*

Por tanto, la distancia focal de la elipse es de 10 cm.

Ejercicio 3

Una elipse tiene sus focos en coordenadas (-2, -1) y (4, -1), halle la distancia focal.

Solución: el ejercicio nos entrega el dato de las posiciones de los focos. Por definición de distancia focal, podemos usar la fórmula de distancia entre dos puntos para obtenerla:

*2c=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}*

*2c=\sqrt{(4-(-2))^2+(-1-(-1))^2}*

*2c=\sqrt{6^2+0^2}*

*2c=\sqrt{6^2}*

*2c=6*

Por tanto, la distancia entre los focos es de 6 unidades.

Ejercicio 4

Encontrar la distancia focal de la elipse cuya ecuación es *2x^2+4x+7y^2-28y-40=0*

Solución: el problema nos da la ecuación general de la elipse, con lo cual no podemos obtener directamente los datos necesarios. Sin embargo, si completamos los cuadrados podemos llegar a la siguiente forma canónica:

*\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1*

De aquí extraemos que:

*a^2=35*

*b^2=10*

Con estos datos usamos la fórmula de distancia focal:

*2c=2\sqrt{a^2-b^2}*

*2c=2\sqrt{35-10}*

*2c=2\sqrt{25}*

*2c=2\cdot 5*

*2c=10*

Por tanto, la distancia focal de esta elipse es de 10 unidades.

Bibliografía

• Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
• Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
• Lehmann, C. (1989). Geometría Analítica. Limusa.
• Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
• Mora, W., y Figueroa, G. (2009). Cónicas. Revista Digital Matemática, Educación e Internet.
• Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
• Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
• Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
• Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.