Vértices de una elipse

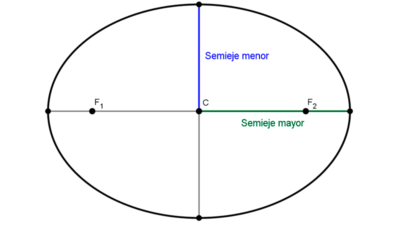
Los vértices de una elipse son los puntos de la misma que están más cerca o más lejos del centro. La elipse tiene cuatro vértices: dos principales, que son los puntos más alejados del centro y extremos del eje mayor; y dos secundarios, que son los puntos más cercanos al centro y extremos del eje menor.

La distancia que separa a los vértices principales es igual a la longitud del eje mayor, 2a, y la distancia que separa a los vértices secundarios es igual al eje menor, 2b. Los vértices principales también suelen llamarse vértices mayores y los secundarios vértices menores o covértices.

A continuación, veremos cómo encontrar los vértices de una elipse con ejercicios resueltos paso a paso.

Cómo hallar los vértices de una elipse

Para obtener las coordenadas de los vértices primero es necesario conocer el centro y las longitudes de los semiejes. Estos datos pueden obtenerse de la ecuación canónica de la elipse, como se muestra en la siguiente tabla.

Orientación	Ecuación	Centro	Vértices principales	Vértices secundarios
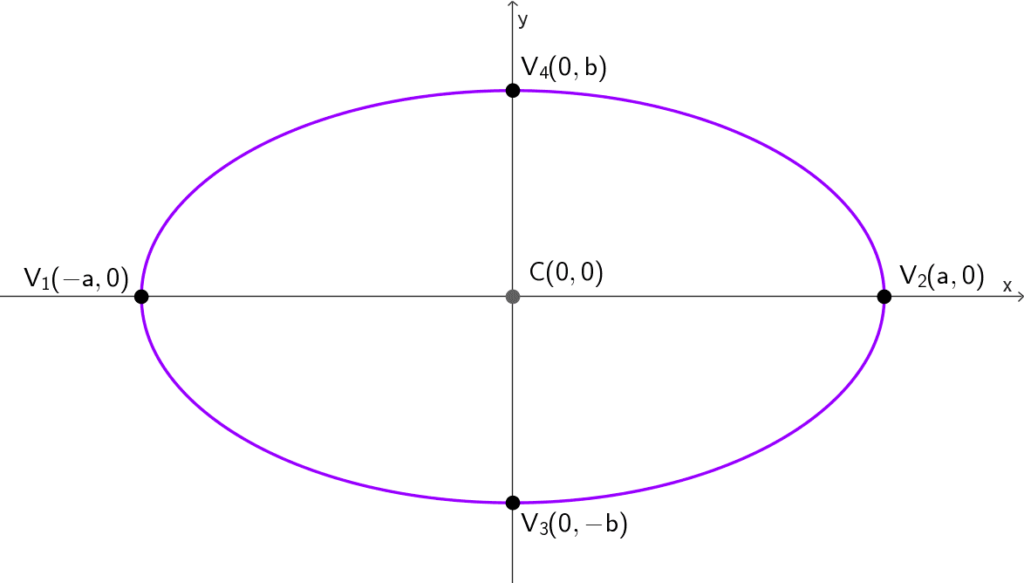
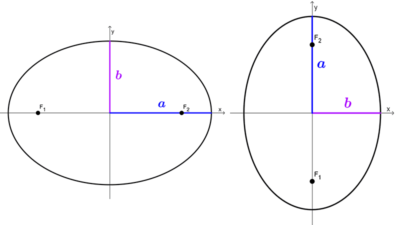
Horizontal	*\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1*	(0, 0)	(-a, 0) y (a, 0)	(0, -b) y (0, b)
Vertical	*\dfrac{x^2}{b^2}+\dfrac{y^2}{a^2}=1*	(0, 0)	(0, -a) y (0, a)	(-b, 0) y (b, 0)
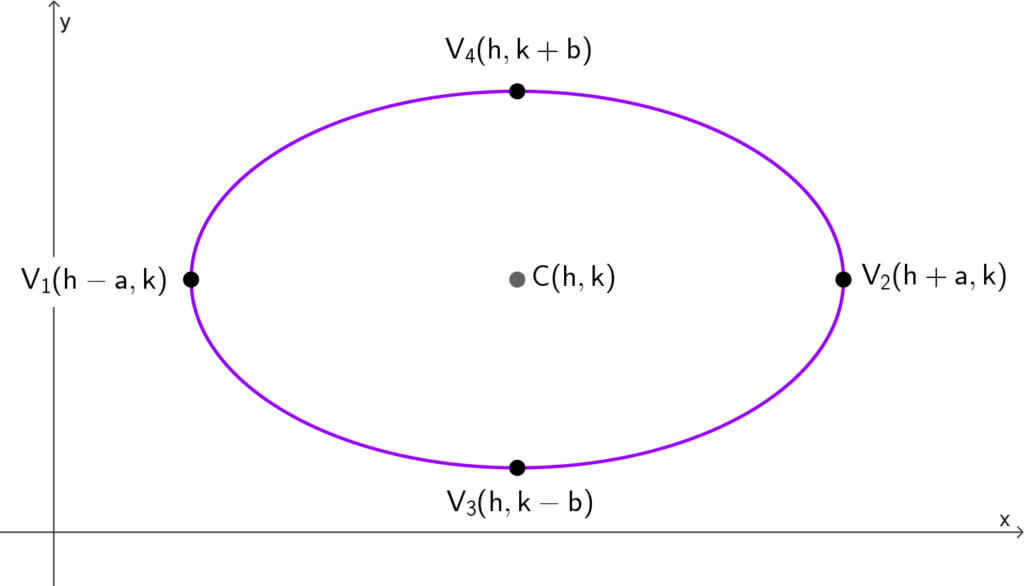
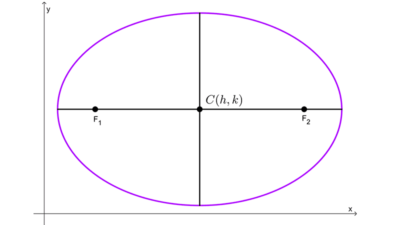
Horizontal	*\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1*	(h, k)	(h - a, k) y (h + a, k)	(h, k - b) y (h, k + b)
Vertical	*\dfrac{(x-h)^2}{b^2}+\dfrac{(y-k)^2}{a^2}=1*	(h, k)	(h, k - a) y (h, k + a)	(h - b, k) y (h + b, k)

Ejercicios resueltos

A continuación, resolvemos algunos ejercicios del cálculo de vértices de una elipse.

Ejercicio 1

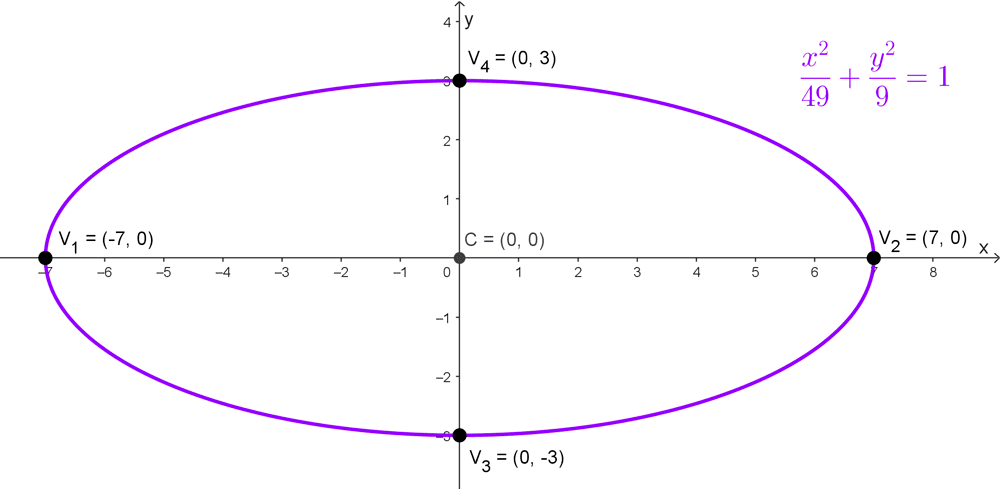
Encontrar los vértices de la elipse *\dfrac{x^2}{49}+\dfrac{y^2}{9}=1*

Solución: primero debemos encontrar el centro de la elipse, de la ecuación sacamos que este es el origen de coordenadas, (0, 0). Ahora necesitamos obtener las longitudes de los los semiejes:

*a^2=49→a=\sqrt{49}=7*

*b^2=9→b=\sqrt{9}=3*

Como el denominador de x² es mayor al denominador de y², la elipse es horizontal. Con el semieje mayor a = 7 obtendremos los vértices principales y con el menor b = 3 los vértices secundarios.

• Vértices principales: (-7, 0) y (7, 0)
• Vértices secundarios: (0, -3) y (0, 3)

Artículos recomendados:

Ejercicio 2 

Determinar cuáles son las coordenadas de los vértices de la elipse que tiene por ecuación *\dfrac{x^2}{4}+\dfrac{y^2}{25}=1*

Solución: de la ecuación canónica obtenemos que el centro es el origen de coordenadas y la elipse es vertical por ser el denominador de y² más grande que el de x². Sacamos los semiejes:

*a^2=25→a=\sqrt{25}=5*

*b^2=4→b=\sqrt{4}=2*

Ahora hallamos los vértices:

• Vértices principales: (0, -5) y (0, 5)
• Vértices secundarios (-2, 0) y (2, 0)

Ejercicio 3

Calcular los vértices mayores y menores de la elipse *\dfrac{(x+2)^2}{10}+\dfrac{(y-3)^2}{18}=1*

Solución: primero determinamos que el centro no es el origen sino el punto (-2, 3) y la elipse es vertical porque 18 > 10. Calculamos los semiejes:

*a^2=18→a=\sqrt{18}*

*b^2=10→b=\sqrt{10}*

Ahora usamos las fórmulas de la tabla para escribir los vértices. Otra forma de hacerlo es graficar la elipse para verlo mejor. El centro es (-2, 3), por lo que h = -2 y k = 3. 

Vértices principales (o mayores): 

• *(h, k - a)=(-2, 3-\sqrt{18})≈(-2; -1,24)*
• *(h, k + a)=(-2, 3+\sqrt{18})≈(-2; 7,24)*

Vértices secundarios (o menores):

• *(h - b, k)=(-2-\sqrt{10}, 3)≈(-5,16; 3)*
• *(h + b, k)=(-2+\sqrt{10}, 3)≈(1,16; 3)*

Ejercicio 4

Hallar los vértices de la elipse *2x^2+4x+7y^2-28y-40=0*

Solución: la ecuación no está en forma canónica sino en forma general, así que primero es necesario completar los cuadrados y reordenarla para obtener la ecuación canónica. Haciendo esto se obtiene:

*\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1*

De aquí se extrae que el centro es (-1, 2) y la elipse es horizontal. Obtenemos los semiejes:

*a^2=35→a=\sqrt{35}*

*b^2=10→b=\sqrt{10}*

Ahora podemos obtener los vértices teniendo en cuenta que h = -1 y k = 2 

Vértices principales:

• *(h - a, k)=(-2-\sqrt{35}; 2)≈(-7,92; 2)*
• *(h + a, k)=(-2+\sqrt{35}; 2)≈(3,92; 2)*

Vértices secundarios:

• *(h, k - b)=(-1; 2-\sqrt{10})≈(-1; -1,16)*
• *(h, k + b)=(-1; 2+\sqrt{10})≈(-1; 5,16)*

Bibliografía

• Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
• Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
• Lehmann, C. (1989). Geometría Analítica. Limusa.
• Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
• Mora, W., y Figueroa, G. (2009). Cónicas. Revista Digital Matemática, Educación e Internet.
• Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
• Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
• Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
• Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.