
Distancia focal de la hipérbola
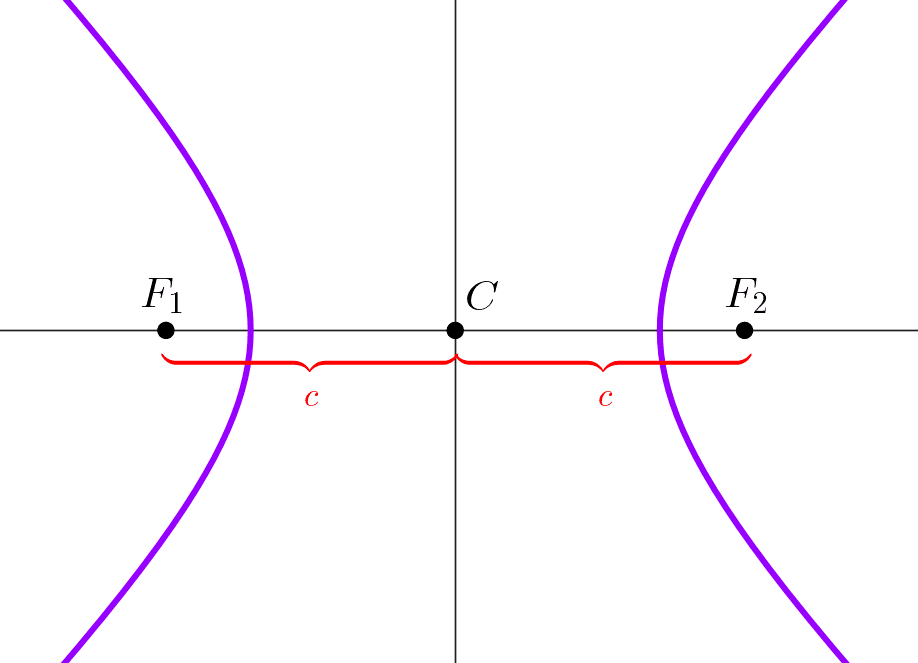
La distancia focal de la hipérbola es la distancia que existe entre sus focos. A la mitad de este valor se le llama semidistancia focal, se simboliza con la letra c y se relaciona con las longitudes de los semiejes a y b por medio de la siguiente fórmula:
c2 = a2 + b2
En toda hipérbola, a diferencia de una elipse, la distancia focal es mayor a la distancia entre los vértices.
Importante: si aún no conoces el significado de la hipérbola en matemáticas, te recomiendo revisar antes el artículo principal donde explicamos su concepto, definición, fórmulas y propiedades.
Cómo calcular la distancia focal
Como vimos antes, la semidistancia focal (c) se relaciona con los semiejes transversal (a) y conjugado (b) mediante la siguiente fórmula:
c2 = a2 + b2
*c=\sqrt{a^2+b^2}*
Esta expresión permite obtener el valor de c a partir de los a y b, los cuales se pueden extraer de la ecuación canónica de la hipérbola. Multiplicando por dos el valor de c, tenemos la distancia focal.
Si se conocen los focos F1(x1, y1) y F2(x2, y2), podemos usar la fórmula de distancia entre dos puntos para hallar la distancia focal:
*2c=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}*
Ejercicios resueltos
Ejercicio 1
Obtener la distancia focal de la hipérbola *\dfrac{x^2}{4}-\dfrac{y^2}{9}=1*
Solución: en la ecuación observamos que la hipérbola tiene su eje transversal a lo largo del eje x, ya que el término positivo es el que contiene a x2. Los valores de a2 y b2 son los denominadores de los términos cuadráticos: *a^2=4~~ y~~ b^2=9.*
Para calcular la semidistancia focal (c), usamos la fórmula:
*c=\sqrt{a^2+b^2}*
Sustituyendo los valores de *a^2~~ y~~ b^2:*
*c=\sqrt{4+9}*
*c=\sqrt{13}*
Por lo tanto, la distancia focal de la hipérbola es el doble de c: *2c=2\sqrt{13}.*
Ejercicio 2
Dada la ecuación de la hipérbola *\dfrac{(y-1)^2}{25}-\dfrac{(x+1)^2}{4}=1* calcular su distancia focal.
Solución: identificamos que la ecuación está en la forma estándar de una hipérbola con eje transversal vertical. El centro de la hipérbola es (-1, 1), y los valores de a2 y b2 son:
*a^2=25*
*b^2=4*
Para hallar la semidistancia focal (c), utilizamos la relación:
*c=\sqrt{a^2+b^2}*
Sustituyendo los valores de *a^2~~ y~~ b^2:*
*c=\sqrt{25+4}=\sqrt{29}*
La distancia focal de la hipérbola es el doble de c, es decir:
*2c=2\sqrt{29}*
Ejercicio 3
Determinar la distancia entre los focos de la hipérbola *\dfrac{x^2}{12}-\dfrac{(y+2)^2}{36}=1*
Solución: identificamos que la ecuación está en la forma estándar de una hipérbola con eje transversal horizontal, su centro es (0, -2), y los valores de a2 y b2 son:
*a^2=12*
*b^2=36*
Para sacar la semidistancia focal (c), usamos la fórmula:
*c=\sqrt{a^2+b^2}*
Sustituyendo los valores de *a^2 ~~y~~ b^2:*
*c=\sqrt{12+36}=\sqrt{48}*
Simplificamos *\sqrt{48}:*
*c=\sqrt{16 \cdot 3}=4\sqrt{3}*
La distancia focal de la hipérbola es el doble de c, es decir:
*2c=2 \cdot 4\sqrt{3}=8\sqrt{3}*
Ejercicio 4
Encontrar la distancia focal de la hipérbola cuya ecuación es *5x^2-2y^2-10x+8y-13=0*
Solución: la ecuación no está en forma canónica así que no podemos sacar directamente las longitudes de los semiejes. Sin embargo, podemos completar los cuadrados para obtener una forma equivalente:
*\dfrac{(x-1)^2}{2}-\dfrac{(y-2)^2}{5}=1*
En primer lugar, identificamos que la ecuación representa una hipérbola con eje transversal horizontal, con centro en (1, 2), y:
*a^2=2~~y~~b^2=5*
Para calcular la semidistancia focal (c), usamos la fórmula:
*c=\sqrt{a^2+b^2}*
Sustituyendo los valores de *a^2~~ y~~ b^2:*
*c=\sqrt{2+5}=\sqrt{7}*
La distancia focal de la hipérbola es el doble de c, es decir:
*2c=2\sqrt{7}*
Bibliografía
- Engler, A. y otros. (2020). Geometría Analítica. Universidad Nacional del Litoral.
- Fuller, G. y Tarwater, D. (1995). Geometría Analítica (7ma edición). Pearson Educación.
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Leithold. L. (1992). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Mora, W., y Figueroa, G. (2009). Cónicas. Revista Digital Matemática, Educación e Internet.
- Márquez, A. y otros. (2009). Geometría Analítica. Prentice Hall.
- Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

Otros artículos que pueden interesarte