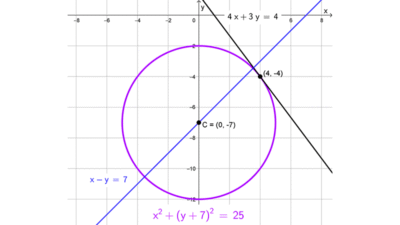
Recta tangente a una circunferencia
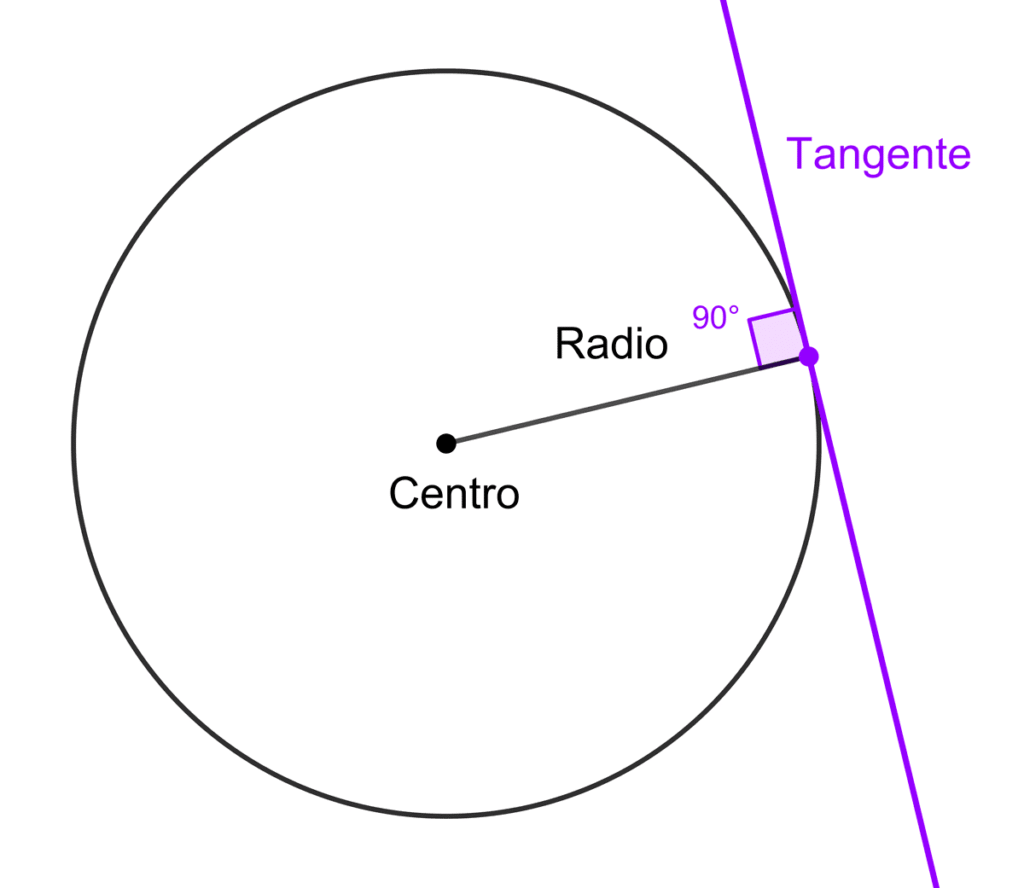
Una recta tangente a una circunferencia es aquella que toca la circunferencia en un único punto, llamado punto de tangencia. En ese punto, la recta es perpendicular al radio que une el centro de la circunferencia con el punto de tangencia.
Índice
Ecuación de la recta tangente
Cuando se estudia la recta tangente a una circunferencia, surgen tres problemas fundamentales que se presentan con frecuencia en geometría analítica:
- Tangente en un punto dado de la circunferencia: se conoce el punto de contacto con la circunferencia y se desea hallar la recta tangente en ese punto.
- Tangente con pendiente dada: se conoce la pendiente de la recta tangente y se desea determinar las tangentes a la circunferencia con esa pendiente.
- Tangente que pasa por un punto exterior: se conoce un punto exterior a la circunferencia, y se buscan las rectas tangentes que pasan por dicho punto.
En cada caso, se emplean enfoques distintos, pero todos se apoyan en la relación geométrica fundamental entre la tangente y el radio: son perpendiculares en el punto de contacto.
Recta tangente dado el punto de contacto
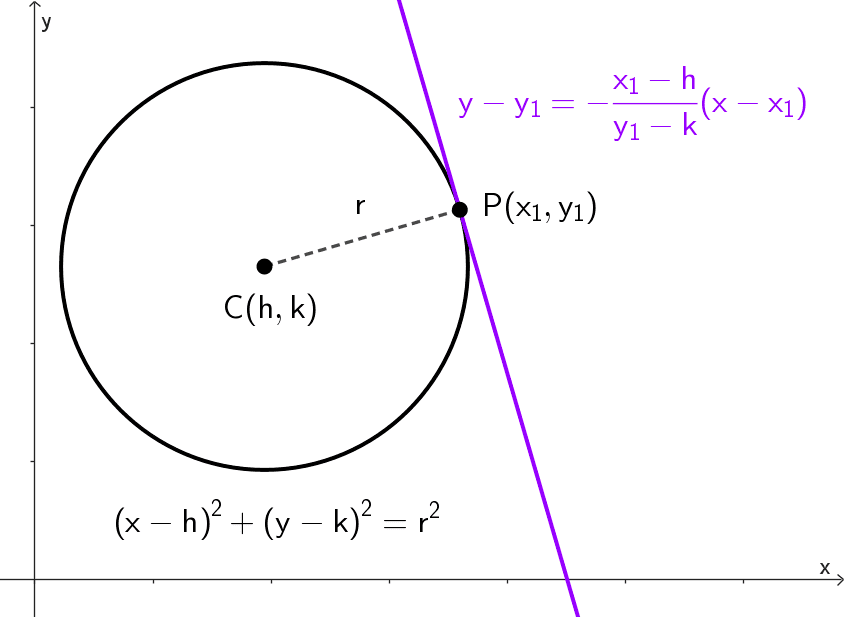
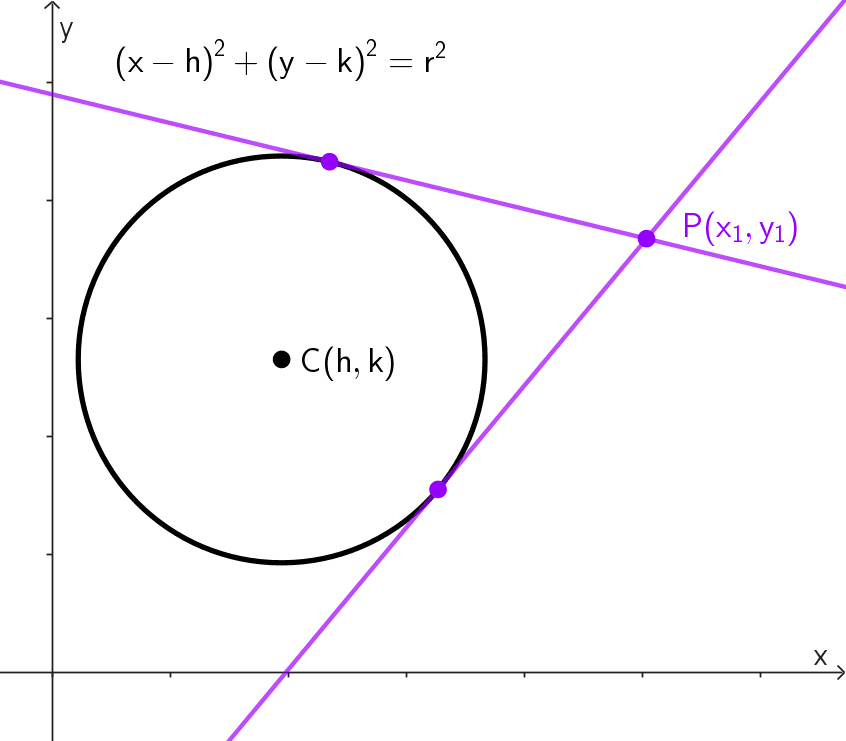
La ecuación de la recta tangente a una circunferencia con centro *C(h, k)* en el punto *P(x_1, y_1)* es:
*y-y_1=-\dfrac{x_1-h}{y_1-k}(x-x_1)*
Procedimiento
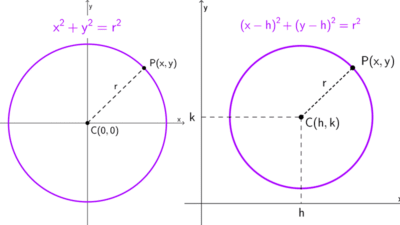
Dada la circunferencia *(x-h)^2+(y-k)^2=r^2* y un punto *P (x_1, y_1)* que pertenece a la circunferencia, la ecuación de la recta tangente en ese punto se puede encontrar así:
1) Calculamos la pendiente del radio que une el centro *C (h, k)* con el punto de contacto *P (x_1, y_1):*
*m_r=\dfrac{y_1-k}{x_1-h}*
2) La recta tangente es perpendicular al radio, por lo tanto, su pendiente será recíproca y opuesta:
*m_t=-\dfrac{1}{m_r}*
3) Escribimos la ecuación de la tangente usando la forma punto-pendiente, con punto *P (x_1, y_1)* y pendiente *m_t*:
*y-y_1=-\dfrac{1}{m_r}(x-x_1)*
Equivalentemente:
*y-y_1=-\dfrac{x_1-h}{y_1-k}(x-x_1)*
Casos especiales
- Si *m_r=0* (es decir, si el punto de tangencia está alineado horizontalmente con el centro), entonces la tangente es vertical (su pendiente no está definida) y su ecuación es *x=x_1.*
- Si *m_r* no está definida (es decir, si *x_1=h*, o sea, el radio es vertical), entonces la pendiente de la tangente es 0 (es horizontal), y su ecuación es: *y=y_1.*
Ejemplos
Hallar la ecuación de la recta tangente a la circunferencia en el punto indicado en cada caso.
- *x^2+y^2=25,* punto P(3, 4).
- *(x-2)^2+(y+1)^2=10,* punto P(3, 2).
- *(x+1)^2+(y-3)^2=8,* punto P(1, 1).
Solución 1
Dada la circunferencia *x^2+y^2=25,* identificamos que su centro es *C(0, 0)* y su radio *r=\sqrt{25}=5.* El punto de tangencia es *P(3, 4).* Calculamos la pendiente del radio *CP:*
*m_r=\dfrac{4-0}{3-0}=\dfrac{4}{3}*
La pendiente de la recta tangente es perpendicular a *m_r,* por lo que:
*m_t=-\dfrac{1}{m_r}=-\dfrac{3}{4}*
Usando la forma punto-pendiente con el punto *P(3, 4)* y *m_t,* obtenemos:
*y-4=-\dfrac{3}{4}(x-3)*
Simplificando:
*4y-16=-3x+9*
*3x+4y-25=0*
Por tanto, la ecuación general de la recta tangente es *\boxed{3x+4y-25=0}*
Solución 2
Para la circunferencia *(x-2)^2+(y+1)^2=10,* el centro es *C(2,-1)* y el radio *r=\sqrt{10}.* El punto de tangencia es *P(3, 2).* Calculamos la pendiente del radio *CP:*
*m_r=\dfrac{2-(-1)}{3-2}=\dfrac{3}{1}=3*
La pendiente de la tangente es:
*m_t=-\dfrac{1}{m_r}=-\dfrac{1}{3}*
Usando la forma punto-pendiente con *P(3, 2):*
*y-2=-\dfrac{1}{3}(x-3)*
Simplificando:
*3y-6=-x+3*
*x+3y-9=0*
La ecuación de la recta tangente es *\boxed{x+3y-9=0}*
Solución 3
En la circunferencia *(x+1)^2+(y-3)^2=8,* el centro es *C(-1, 3)* y el radio *r=2\sqrt{2}.* El punto de tangencia es *P(1, 1).* Calculamos la pendiente del radio *CP:*
*m_r=\dfrac{1-3}{1-(-1)}=\dfrac{-2}{2}=-1*
La pendiente de la tangente es:
*m_t=-\dfrac{1}{m_r}=-\dfrac{1}{-1}=1*
Usando la forma punto-pendiente con *P(1, 1):*
*y-1=1(x-1)*
Simplificando:
*y-1=x-1*
*x-y=0*
La ecuación de la recta tangente es *\boxed{x-y=0}*
El siguiente recurso te permite calcular la ecuación de la recta tangente pudiendo cambiar la ecuación de la circunferencia y el punto de contacto.
Recta tangente con una pendiente dada
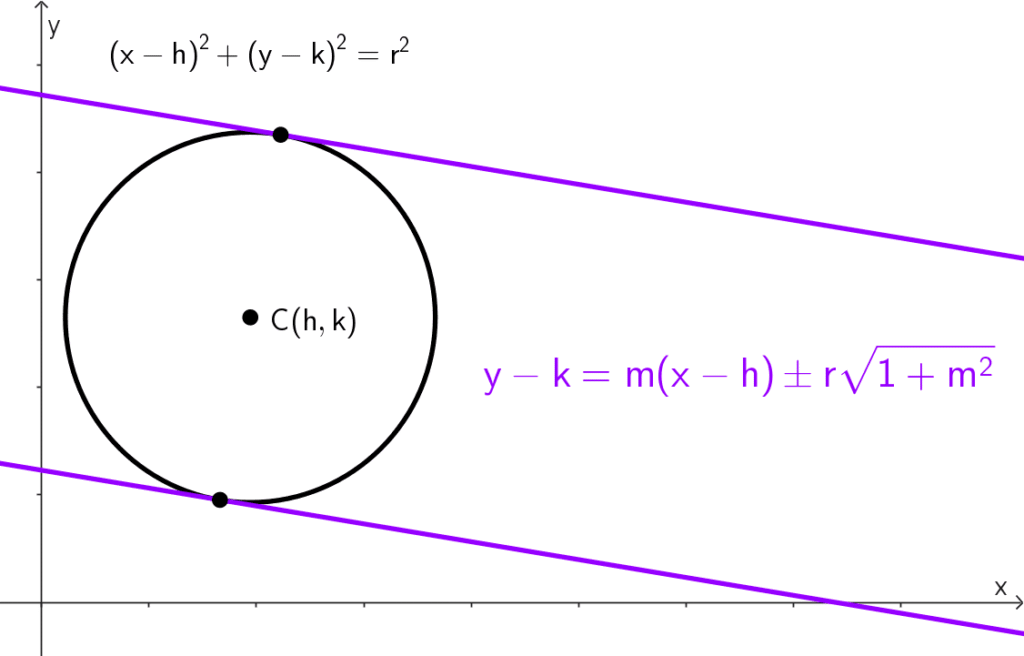
La ecuación de la recta con pendiente m que es tangente a una circunferencia con centro en C(h, k) y radio r es:
*y-k=m (x-h) \pm r \sqrt{1+m^2}*
En general, hay dos tangentes con pendiente m a una circunferencia, correspondientes a los dos signos de la raíz cuadrada.
Procedimiento
Tenemos la circunferencia *(x-h)^2+(y-k)^2=r^2* y una pendiente *m*, y queremos hallar las rectas tangentes a la circunferencia que tengan exactamente esa pendiente.
1) Planteamos la ecuación explícita de una recta con pendiente *m*:
*y=mx+b*
donde *b* es un parámetro a determinar.
2) Imponemos la condición de tangencia: para que esta recta sea tangente a la circunferencia, la distancia del centro *(h, k)* a la recta debe ser igual al radio *r*. Aplicamos la fórmula de distancia punto-recta:
*\dfrac{|mh-k+b|}{\sqrt{1+m^2}}=r*
3) Despejamos *b:*
Multiplicamos ambos lados por *\sqrt{1+m^2}*:
*|mh-k+b|=r \sqrt{1+m^2}*
Esto se traduce en dos posibilidades (por el valor absoluto):
*mh-k+b=\pm r \sqrt{1+m^2}*
Finalmente, despejamos *b*:
*b=k-mh \pm r \sqrt{1+m^2}*
4) Usamos los valores encontrados para *b* en la ecuación *y=mx+b.* Las dos rectas tangentes resultantes son:
*y=mx+\left (k-mh+r \sqrt{1+m^2} \right) \quad \text{y} \quad y=mx+\left (k-mh-r \sqrt{1+m^2} \right)*
Ejemplos
Encontrar las ecuaciones de las rectas tangentes a las siguientes circunferencias dada la pendiente. Además, determinar los puntos de tangencia.
- Circunferencia: *(x-1)^2+(y+2)^2=9,* pendiente: *m=2.*
- Circunferencia: *x^2+y^2=16,* pendiente *m=-\dfrac{3}{4}.*
- Circunferencia: *x^2+y^2-6x+4y-3=0,* pendiente: *m=1.*
- Circunferencia: *(x+3)^2+(y-1)^2=15,* pendiente *m=-2.*
Solución 1
Dada la circunferencia *(x-1)^2+(y+2)^2=9,* identificamos el centro *C(1,-2)* y el radio *r=3.* La pendiente requerida es *m=2.* Aplicamos la fórmula para hallar el término independiente *b* de la recta tangente *y=2x+b:*
*b=k-mh ± r\sqrt{1+m^2}=-2-2(1) ± 3\sqrt{1+2^2}=-4 ± 3\sqrt{5}*
Las ecuaciones de las rectas tangentes son:
*y=2x-4+3\sqrt{5} \quad \text{y} \quad y=2x-4-3\sqrt{5}*
Para hallar los puntos de tangencia, sustituimos *y=2x+b* en la ecuación de la circunferencia y resolvemos el sistema. Sin embargo, dado que ya impusimos la condición de tangencia, los puntos de contacto están en la intersección de las rectas tangentes con la perpendicular que pasa por el centro.
La recta perpendicular es la misma para ambos puntos de tangencia y tiene ecuación:
*y+2=-\dfrac{1}{2}(x-1) → x+2y+3=0*
Para *b=-4+3\sqrt{5}:*
Sustituimos *y=2x-4+3\sqrt{5}* en *x+2y+3=0:*
*x+2(2x-4+3\sqrt{5})+3=0 → x+4x-8+6\sqrt{5}+3=0*
*5x-5+6\sqrt{5}=0 → 5x=5-6\sqrt{5} → x=\dfrac{5-6\sqrt{5}}{5}*
Ahora, calculamos *y:*
*y=2\left(\dfrac{5-6\sqrt{5}}{5}\right)-4+3\sqrt{5}=\dfrac{10-12\sqrt{5}}{5}-4+3\sqrt{5}*
*y=\dfrac{10-12\sqrt{5}-20}{5}+3\sqrt{5}=\dfrac{-10-12\sqrt{5}}{5}+3\sqrt{5}*
*y=-2-\dfrac{12\sqrt{5}}{5}+3\sqrt{5}=-2+\left(-\dfrac{12}{5}+3\right)\sqrt{5}*
*y=-2+\dfrac{3}{5}\sqrt{5}*
Para *b=-4-3\sqrt{5}:*
Sustituimos *y=2x-4-3\sqrt{5}* en *x+2y+3=0:*
*x+2(2x-4-3\sqrt{5})+3=0 → x+4x-8-6\sqrt{5}+3=0*
*5x-5-6\sqrt{5}=0 → 5x=5+6\sqrt{5} → x=\dfrac{5+6\sqrt{5}}{5}*
Calculamos *y:*
*y=2\left(\dfrac{5+6\sqrt{5}}{5}\right)-4-3\sqrt{5}=\dfrac{10+12\sqrt{5}}{5}-4-3\sqrt{5}*
*y=\dfrac{10+12\sqrt{5}-20}{5}-3\sqrt{5}=\dfrac{-10+12\sqrt{5}}{5}-3\sqrt{5}*
*y=-2+\dfrac{12\sqrt{5}}{5}-3\sqrt{5}=-2+\left(\dfrac{12}{5}-3\right)\sqrt{5}*
*y=-2-\dfrac{3}{5}\sqrt{5}*
Puntos de tangencia:
*\left(\dfrac{5-6\sqrt{5}}{5},-2+\dfrac{3\sqrt{5}}{5}\right) ≈ (-1,68; -0.66)*
*\left(\dfrac{5+6\sqrt{5}}{5},-2-\dfrac{3\sqrt{5}}{5}\right) ≈ (3,68; -3,34)*
Solución 2
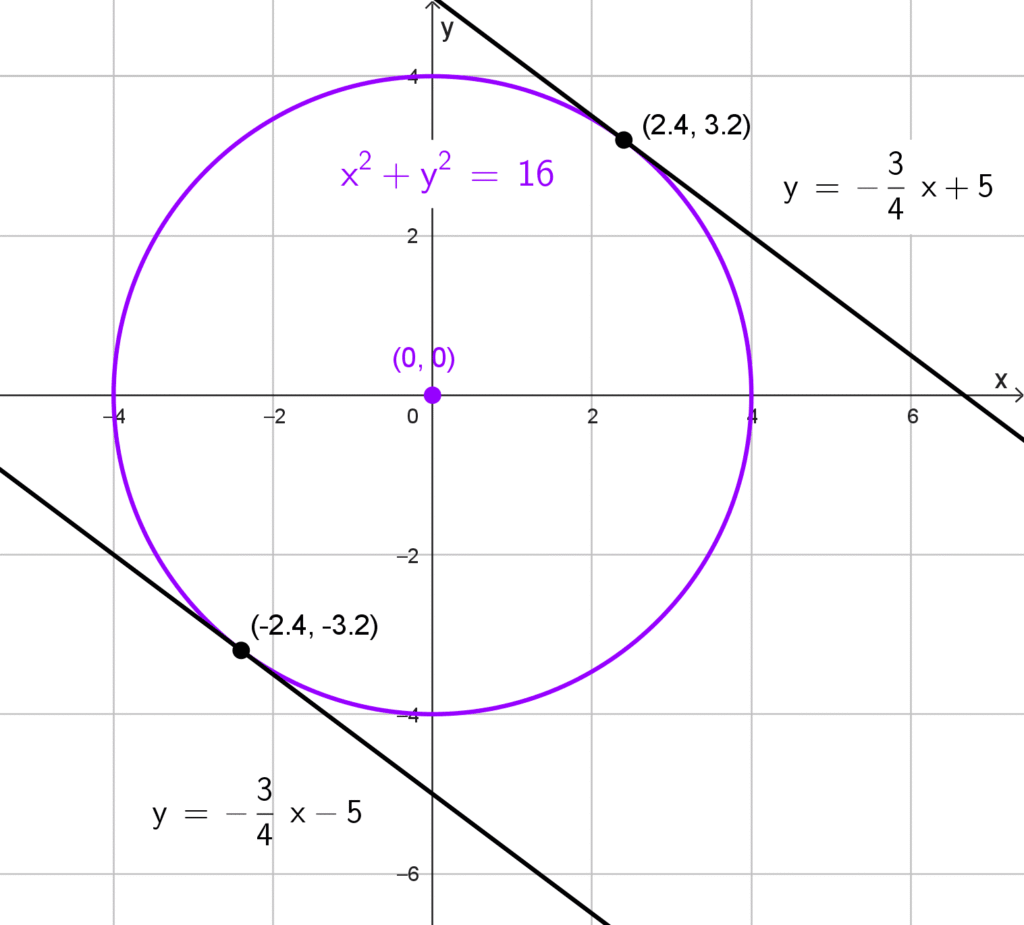
Para la circunferencia *x^2+y^2=16,* el centro es *C(0, 0)* y el radio *r=4.* La pendiente dada es *m=-\dfrac{3}{4}.* Calculamos *b:*
*b=0-\left(-\dfrac{3}{4}\right)(0) ± 4\sqrt{1+\left(-\dfrac{3}{4}\right)^2}=± 4 \cdot \dfrac{5}{4}=± 5*
Las ecuaciones de las tangentes son:
*y=-\dfrac{3}{4}x+5 \quad \text{y} \quad y=-\dfrac{3}{4}x-5*
Puntos de tangencia:
Para *b=5,* la recta perpendicular tiene pendiente *\dfrac{4}{3}* y pasa por *C(0, 0):*
*y=\dfrac{4}{3}x*
Resolviendo el sistema con *y=-\dfrac{3}{4}x+5,* obtenemos:
*x=\dfrac{12}{5}=2,4 \quad y=\dfrac{16}{5}=3,2*
Para *b=-5,* el punto es:
*x=-\dfrac{12}{5}=-2,4 \quad y=-\dfrac{16}{5}=-3,2*
Por tanto, los puntos de intersección son:
*\left(\dfrac{12}{5}, \dfrac{16}{5}\right) \quad \text{y} \quad \left(-\dfrac{12}{5},-\dfrac{16}{5}\right)*
Solución 3
La ecuación *x^2+y^2-6x+4y-3=0* se completa cuadrados para obtener:
*(x-3)^2+(y+2)^2=16*
El centro es *C(3,-2)* y el radio *r=4.* La pendiente dada es *m=1.* Calculamos *b:*
*b=-2-1(3) ± 4\sqrt{1+1^2}=-5 ± 4\sqrt{2}*
Las ecuaciones de las tangentes son:
*y=x-5+4\sqrt{2} \quad \text{y} \quad y=x-5-4\sqrt{2}*
Puntos de tangencia:
Para *b=-5+4\sqrt{2},* la recta perpendicular tiene pendiente *-1* y pasa por *C(3,-2):*
*y+2=-1(x-3) → x+y-1=0*
Resolviendo el sistema con *y=x-5+4\sqrt{2},* obtenemos:
*x=3-2\sqrt{2}, \quad y=-2+2\sqrt{2}*
Para *b=-5-4\sqrt{2},* el punto es:
*x=3+2\sqrt{2}, \quad y=-2-2\sqrt{2}*
Por tanto, los puntos de tangencia son:
*\left(3-2\sqrt{2},-2+2\sqrt{2}\right)≈(0,17; 0,83)*
*\left(3+2\sqrt{2},-2-2\sqrt{2}\right)≈(5,83; -4,83)*
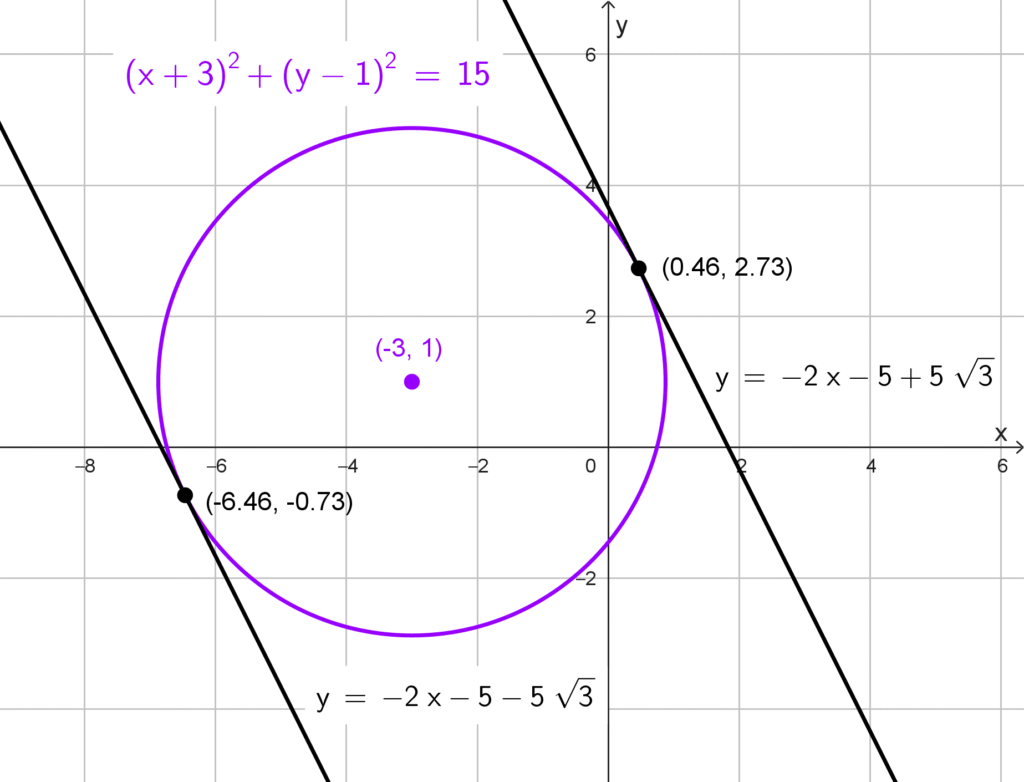
Solución 4
Dada *(x+3)^2+(y-1)^2=15,* el centro es *C(-3, 1)* y el radio *r=\sqrt{15}.* La pendiente es *m=-2.* Calculamos *b:*
*b=1-(-2)(-3) ± \sqrt{15} \cdot \sqrt{1+(-2)^2}=-5 ± \sqrt{75}=-5 ± 5\sqrt{3}*
Las ecuaciones de las tangentes son:
*y=-2x-5+5\sqrt{3} \quad \text{y} \quad y=-2x-5-5\sqrt{3}*
Puntos de tangencia
La recta perpendicular que pasa por C(-3, 1) con pendiente *\dfrac{1}{2}* es:
*y-1=\dfrac{1}{2}(x+3) → x-2y+5=0*
Resolvemos el sistema entre la recta tangente y la perpendicular.
Para *b=-5+5\sqrt{3}:*
Sustituimos *y=-2x-5+5\sqrt{3}* en *x-2y+5=0:*
*x-2(-2x-5+5\sqrt{3})+5=0 → x+4x+10-10\sqrt{3}+5=0*
*5x+15-10\sqrt{3}=0 → 5x=-15+10\sqrt{3} → x=-3+2\sqrt{3}*
Ahora calculamos *y:*
*y=-2(-3+2\sqrt{3})-5+5\sqrt{3}=6-4\sqrt{3}-5+5\sqrt{3}=1+\sqrt{3}*
Para *b=-5-5\sqrt{3}:*
Sustituimos *y=-2x-5-5\sqrt{3}* en *x-2y+5=0:*
*x-2(-2x-5-5\sqrt{3})+5=0 → x+4x+10+10\sqrt{3}+5=0*
*5x+15+10\sqrt{3}=0 → 5x=-15-10\sqrt{3} → x=-3-2\sqrt{3}*
Ahora calculamos *y:*
*y=-2(-3-2\sqrt{3})-5-5\sqrt{3}=6+4\sqrt{3}-5-5\sqrt{3}=1-\sqrt{3}*
En conclusión, los puntos de tangencia son:
*\left(-3+2\sqrt{3}, 1+\sqrt{3}\right)≈(0,46; 2,73)*
*\left(-3-2\sqrt{3}, 1-\sqrt{3}\right)≈(-6.46,-0.73)*
Con el siguiente recurso puedes modificar la ecuación de la circunferencia y la pendiente dada para obtener las ecuaciones de las tangentes y los puntos de contacto en el gráfico.
Recta tangente desde un punto exterior
Desde un punto exterior a una circunferencia se pueden trazar dos rectas tangentes a la circunferencia. Los puntos de tangencia no serán los mismos para ambas rectas. Dada una circunferencia de ecuación *(x-h)^2+(y-k)^2=r^2* y un punto *P(x_1, y_1)* exterior a ella, para encontrar las ecuaciones de las tangentes debemos seguir el siguiente procedimiento:
1) Planteamos la ecuación de la recta que pasa por el punto exterior *P(x_1, y_1)*:
*y=m (x-x_1)+y_1*
2) Sustituimos en la ecuación de la circunferencia:
*(x-h)^2+\left[m (x-x_1)+y_1-k\right]^2=r^2*
3) Desarrollamos y reducimos a una ecuación cuadrática en x. Luego igualamos el discriminante a cero (para que haya un solo punto de intersección, lo que equivale a tangencia).
4) Resolvemos esta ecuación para *m:* eso nos da las pendientes de las dos tangentes.
5) Sustituimos cada valor de *m* en la ecuación *y-y_1=m (x-x_1)* para obtener las dos rectas tangentes.
Ejemplos
Obtener las ecuaciones de las rectas tangentes a las siguientes circunferencias dado un punto exterior:
- Circunferencia: *(x+3)^2+(y-2)^2=10;* punto: P(0, 5).
- Circunferencia *x^2+y^2-6x+4y-12=0,* punto P(-1, 3).
Solución 1
Dada la circunferencia *(x+3)^2+(y-2)^2=10* y el punto exterior *P(0, 5),* la ecuación de la recta que pasa por P es *y-5=m(x-0).* Sustituimos *y=mx+5* en la ecuación de la circunferencia:
*(x+3)^2+(mx+5-2)^2=10*
Simplificamos:
*(x+3)^2+(mx+3)^2=10*
Desarrollamos ambos cuadrados:
*x^2+6x+9+m^2x^2+6mx+9=10*
Agrupamos términos:
*(1+m^2)x^2+(6+6m)x+8=0*
Para que la recta sea tangente, el discriminante debe ser cero. El discriminante *\Delta* de *Ax^2+Bx+C=0* es *\Delta=B^2-4AC,* en donde *A=1+m^2, B=6+6m* y *C=8.* Calculamos:
*(6+6m)^2-4(1+m^2)(8)=0*
Expandimos:
*36+72m+36m^2-32-32m^2=0 \quad → \quad 4m^2+72m+4=0*
Simplificamos:
*m^2+18m+1=0*
Resolviendo:
*m=\dfrac{-18±\sqrt{324-4}}{2}=\dfrac{-18±\sqrt{320}}{2}=-9±4\sqrt{5}*
Con esto obtuvimos los valores de las pendientes. Por lo tanto, las ecuaciones de las tangentes son:
*y-5=(-9+4\sqrt{5})x \quad \text{y} \quad y-5=(-9-4\sqrt{5})x*
Solución 2
Primero reescribimos la ecuación *x^2+y^2-6x+4y-12=0* en forma estándar completando cuadrados:
*x^2-6x+y^2+4y=12 \quad → \quad (x-3)^2-9+(y+2)^2-4=12*
Simplificamos:
*(x-3)^2+(y+2)^2=25*
El punto *P(-1, 3)* está fuera de la circunferencia. La ecuación de la recta que pasa por *P* es *y-3=m(x+1).* Sustituimos *y=m(x+1)+3* en la ecuación de la circunferencia:
*(x-3)^2+\left[m(x+1)+3+2\right]^2=25*
Simplificamos:
*(x-3)^2+\left[m(x+1)+5\right]^2=25*
Desarrollamos:
*x^2-6x+9+m^2(x+1)^2+10m(x+1)+25=25*
Expandimos:
*x^2-6x+9+m^2x^2+2m^2x+m^2+10mx+10m=0*
Agrupamos términos:
*(1+m^2)x^2+(-6+2m^2+10m)x+(9+m^2+10m)=0*
Igualamos el discriminante a cero:
*(-6+2m^2+10m)^2-4(1+m^2)(9+m^2+10m)=0*
Expandimos y simplificamos:
*36+4m^4+100m^2-24m^2-120m+40m^3-36-4m^2-40m-36m^2-4m^4-40m^3=0*
Reducimos:
*36m^2-160m=0 \quad → \quad 4m(9m-40)=0*
Las soluciones son *m=0* y *m=\dfrac{40}{9}.* Las ecuaciones de las tangentes son:
*y-3=0(x+1) \quad → \quad y=3*
y
*y-3=\dfrac{40}{9}(x+1)*
Con el siguiente recurso de GeoGebra puedes obtener las ecuaciones de las tangentes modificando la ecuación de la circunferencia y el punto exterior.
Bibliografía
- Lehmann, C. (1989). Geometría Analítica. Limusa.
- Raichman, S. y Totter, E. (2016). Geometría Analítica para Ciencias e Ingeniería. Universidad Nacional de Cuyo.
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

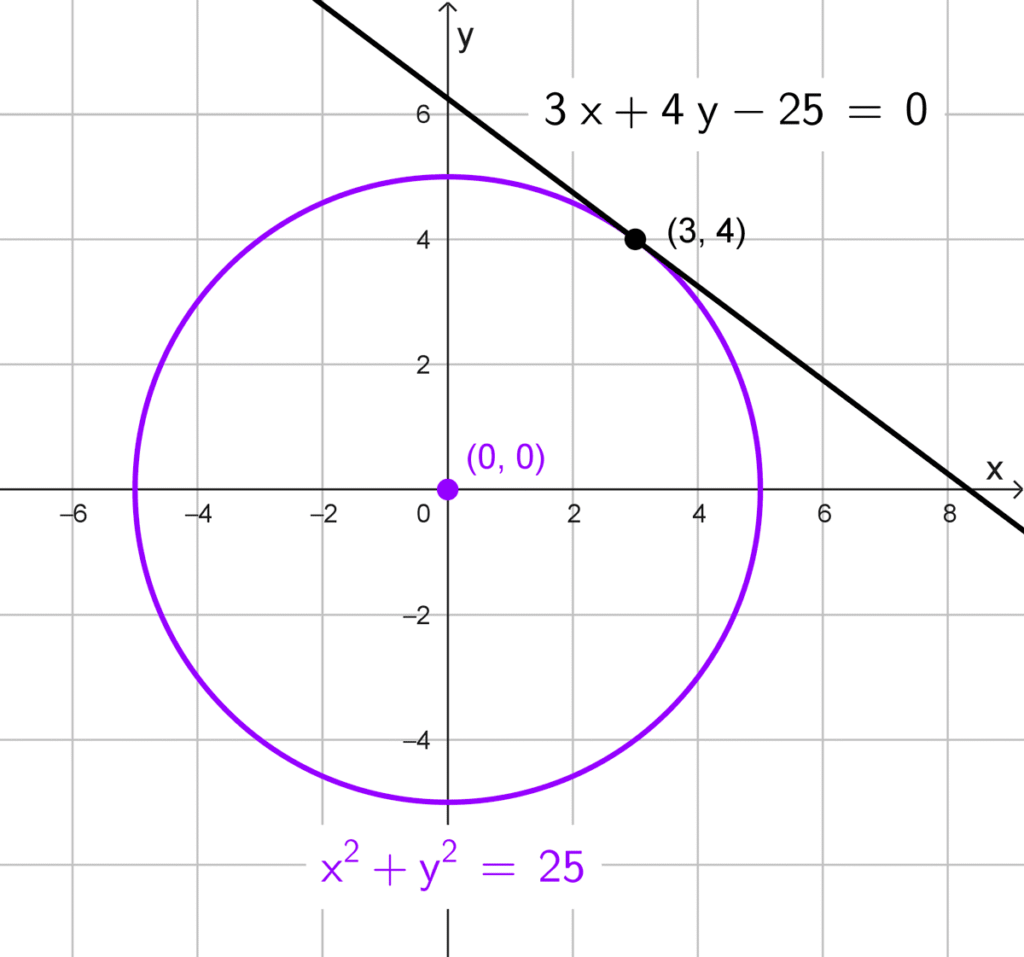
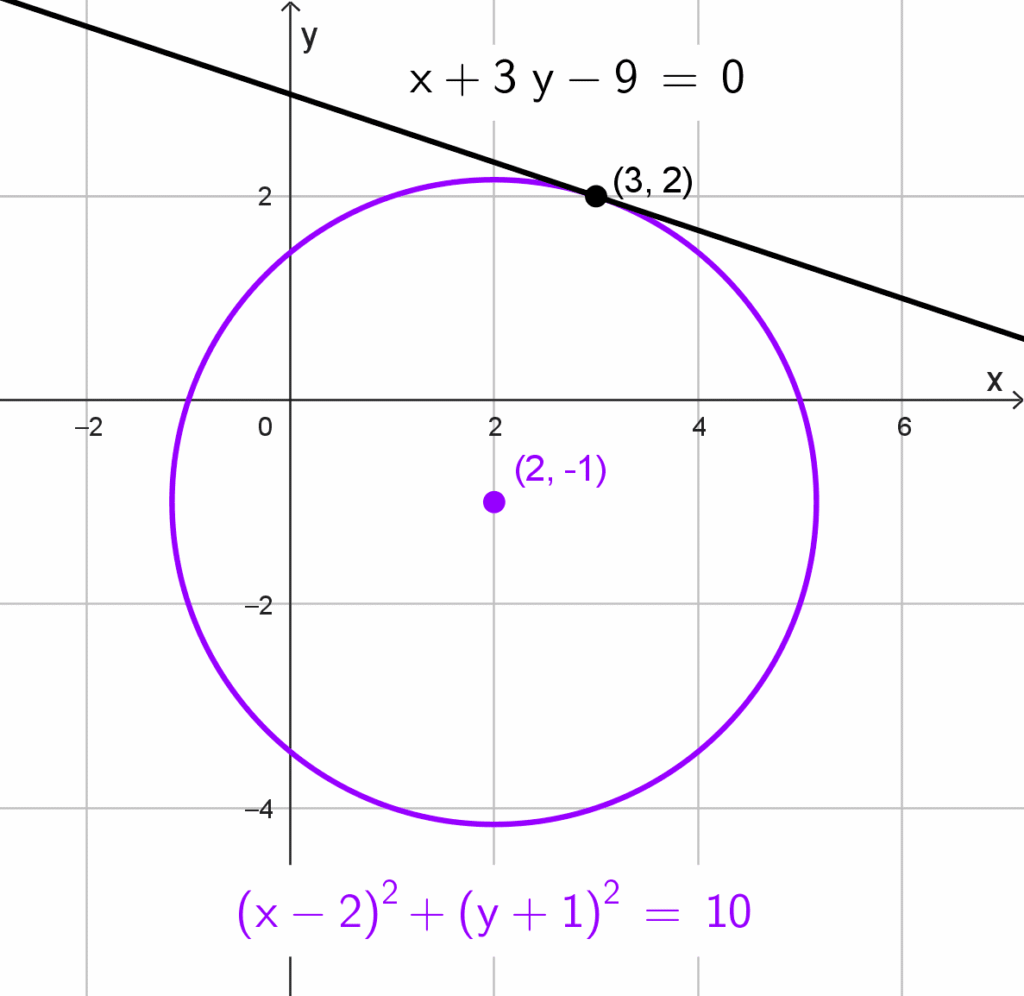
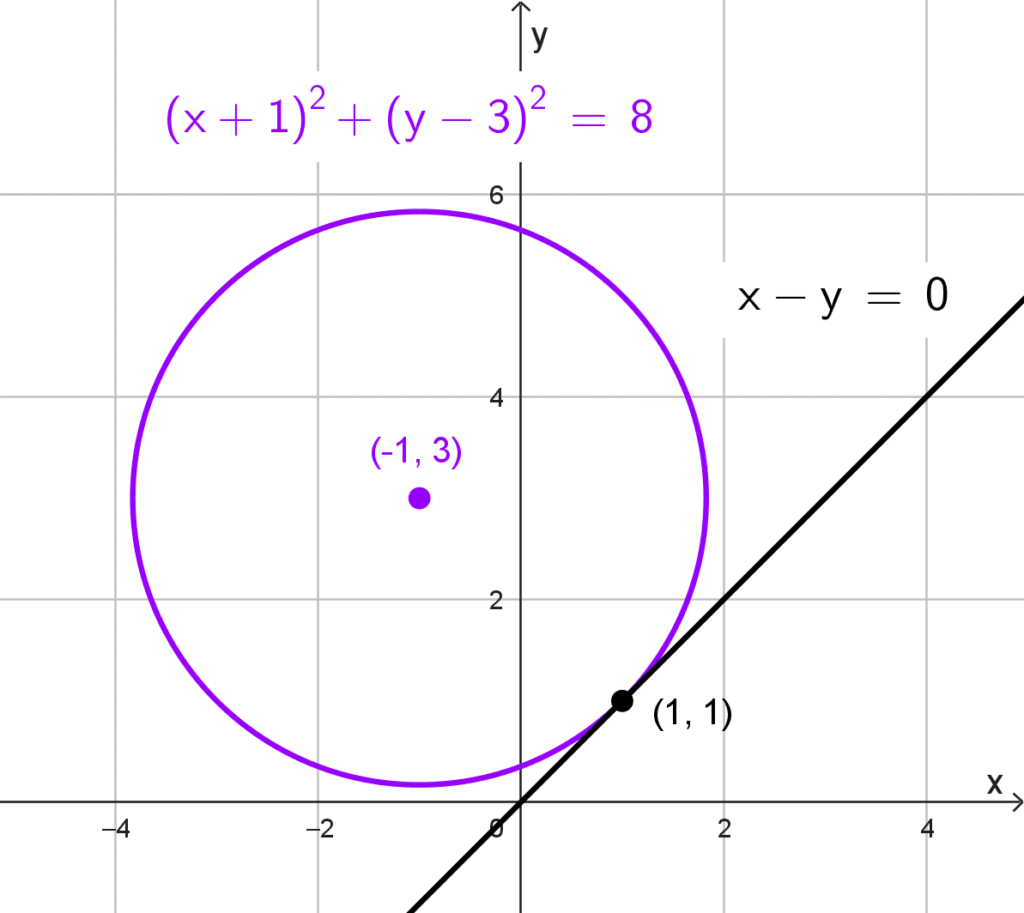
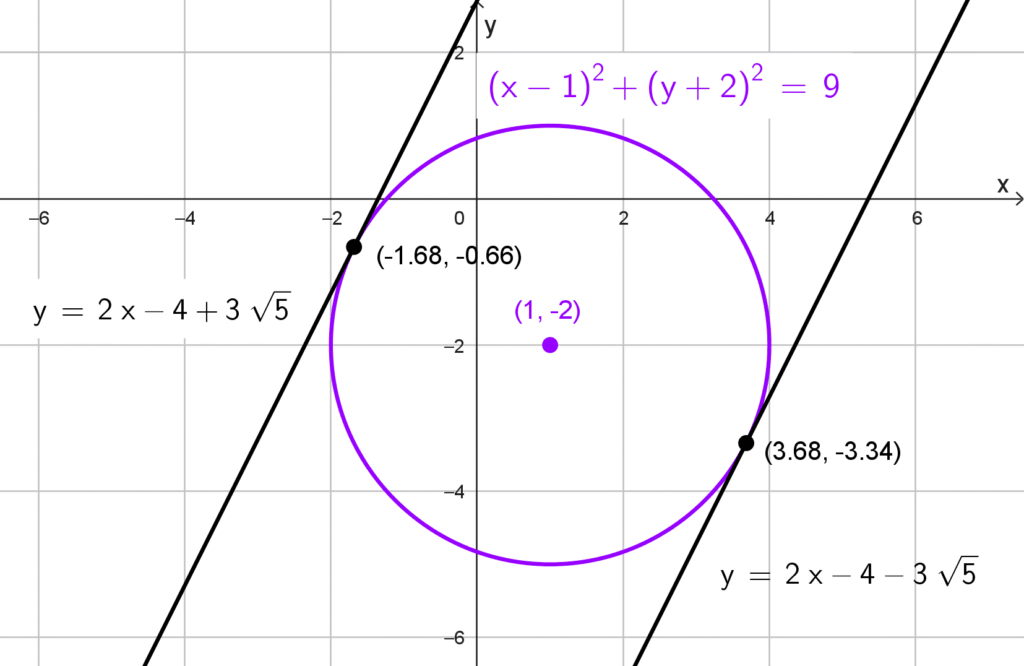
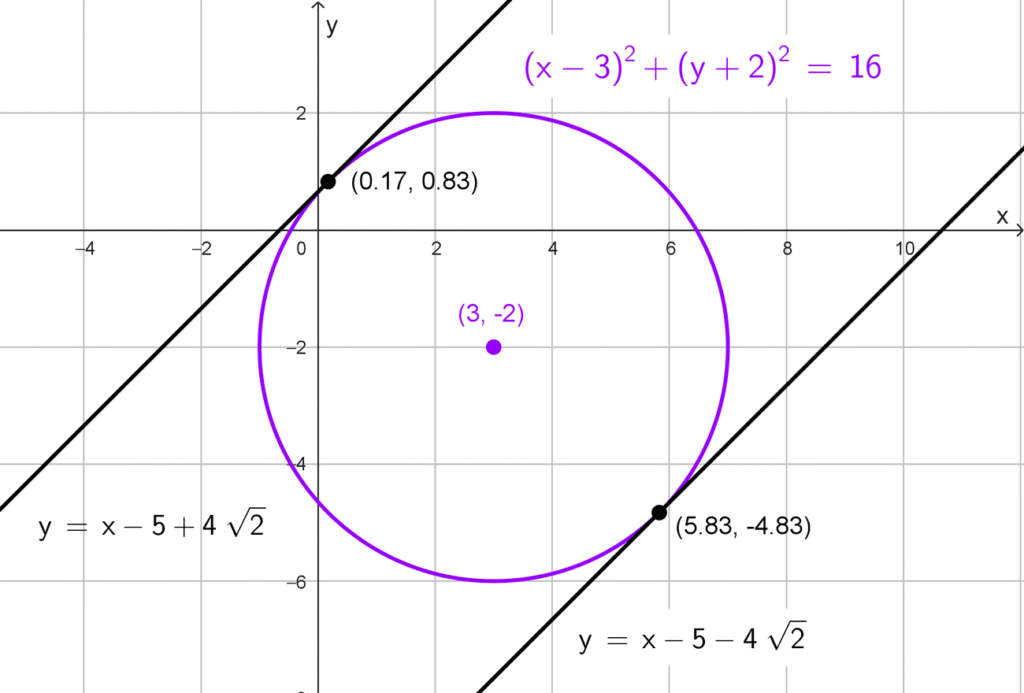
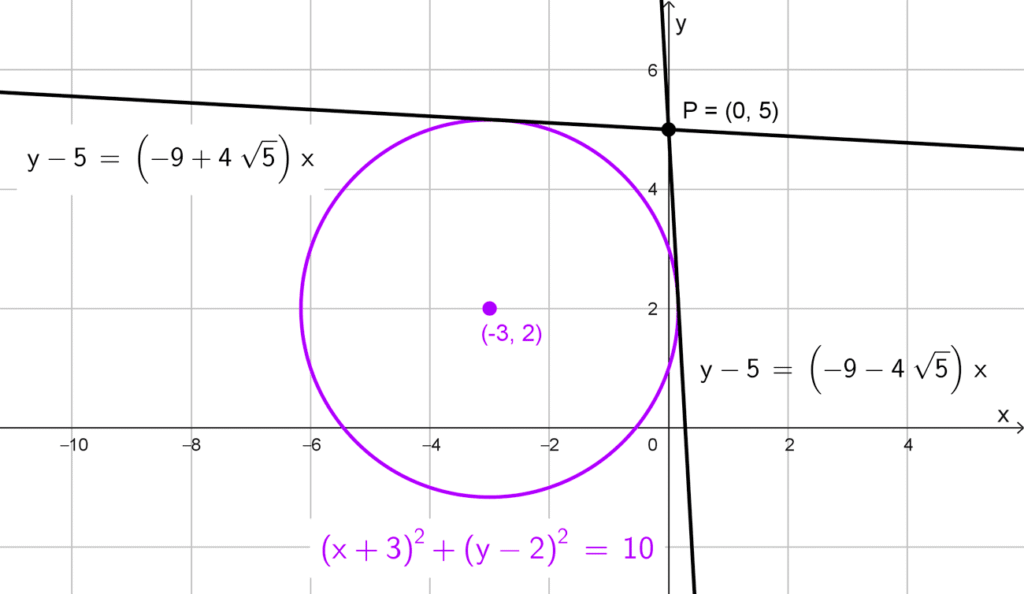
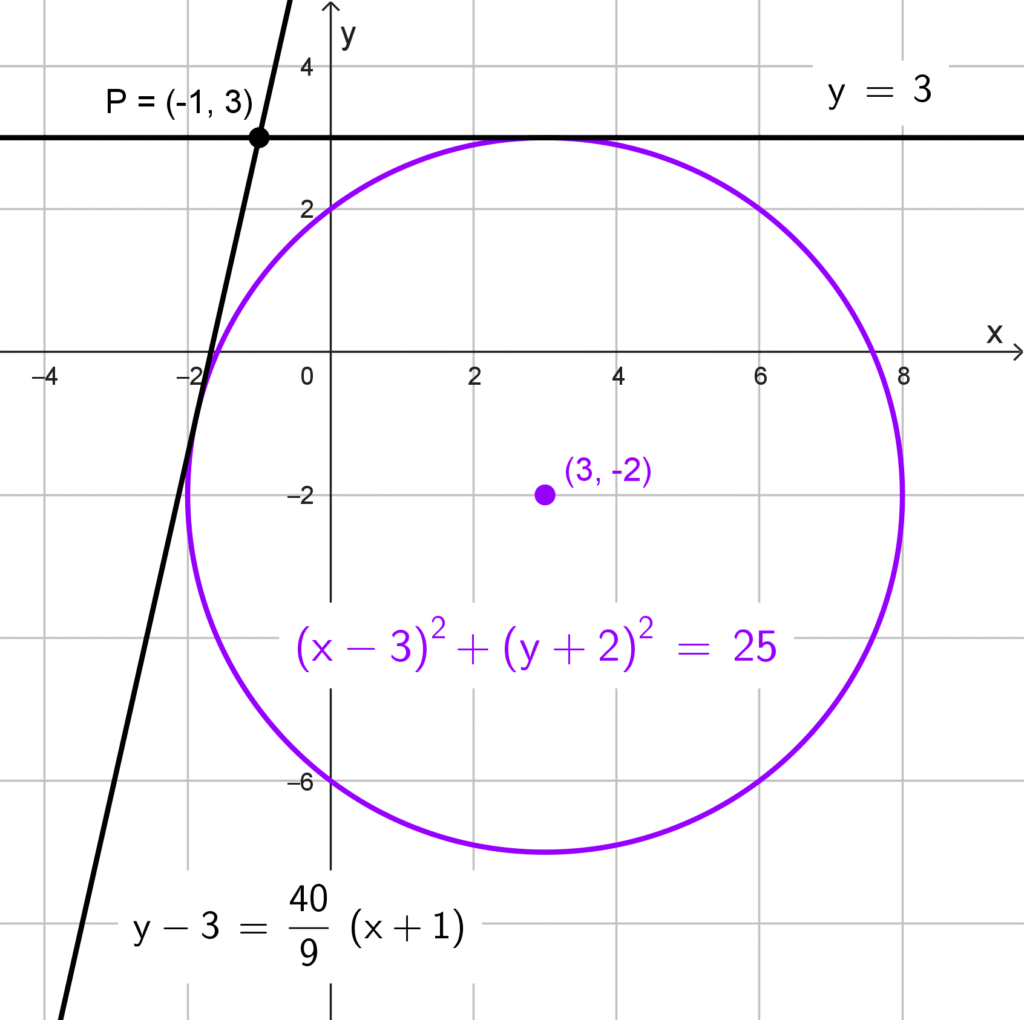


Otros artículos que pueden interesarte