Puntos, segmentos y rectas notables de una circunferencia
Los puntos, segmentos y rectas notables de una circunferencia son el centro, el radio, el diámetro, las cuerdas, las rectas tangentes y las rectas secantes, entre otros. A continuación, veremos la descripción de cada uno.
Índice
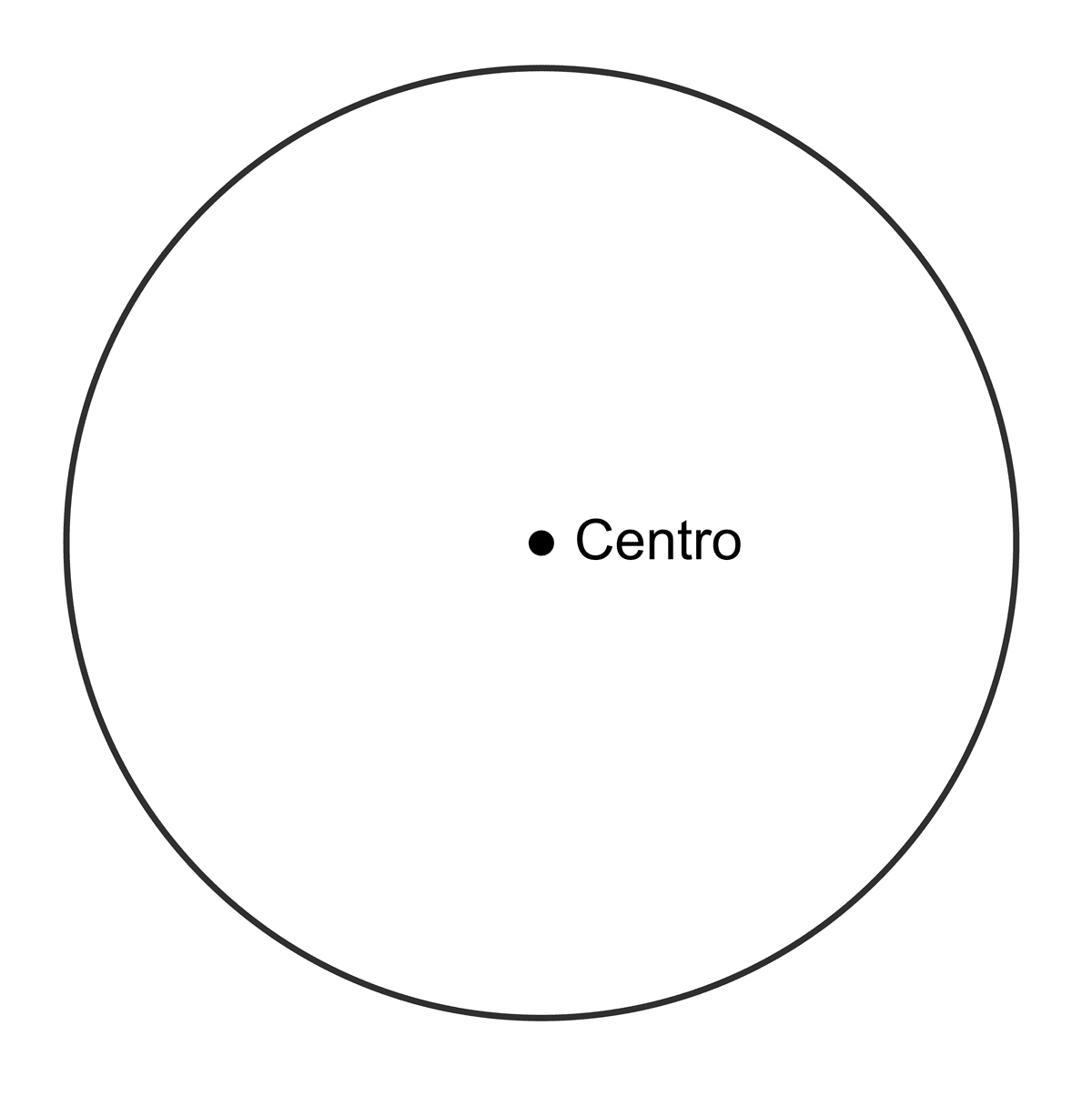
Centro
El centro de la circunferencia es el punto equidistante de todos los puntos de la curva. Se denota comúnmente como C(h, k). Es el punto de referencia para definir el radio y para establecer la ecuación de la circunferencia en forma estándar:
\((x-h)^2+(y-k)^2=r^2\)
Ejemplos
- La circunferencia \((x-2)^2+(y+3)^2=16\) tiene su centro en (2, -3).
- La circunferencia \((x+5)^2+(y-1)^2=25\) tiene su centro en (-5, 1).
- La circunferencia \(x^2+y^2=9\) tiene su centro en (0, 0).
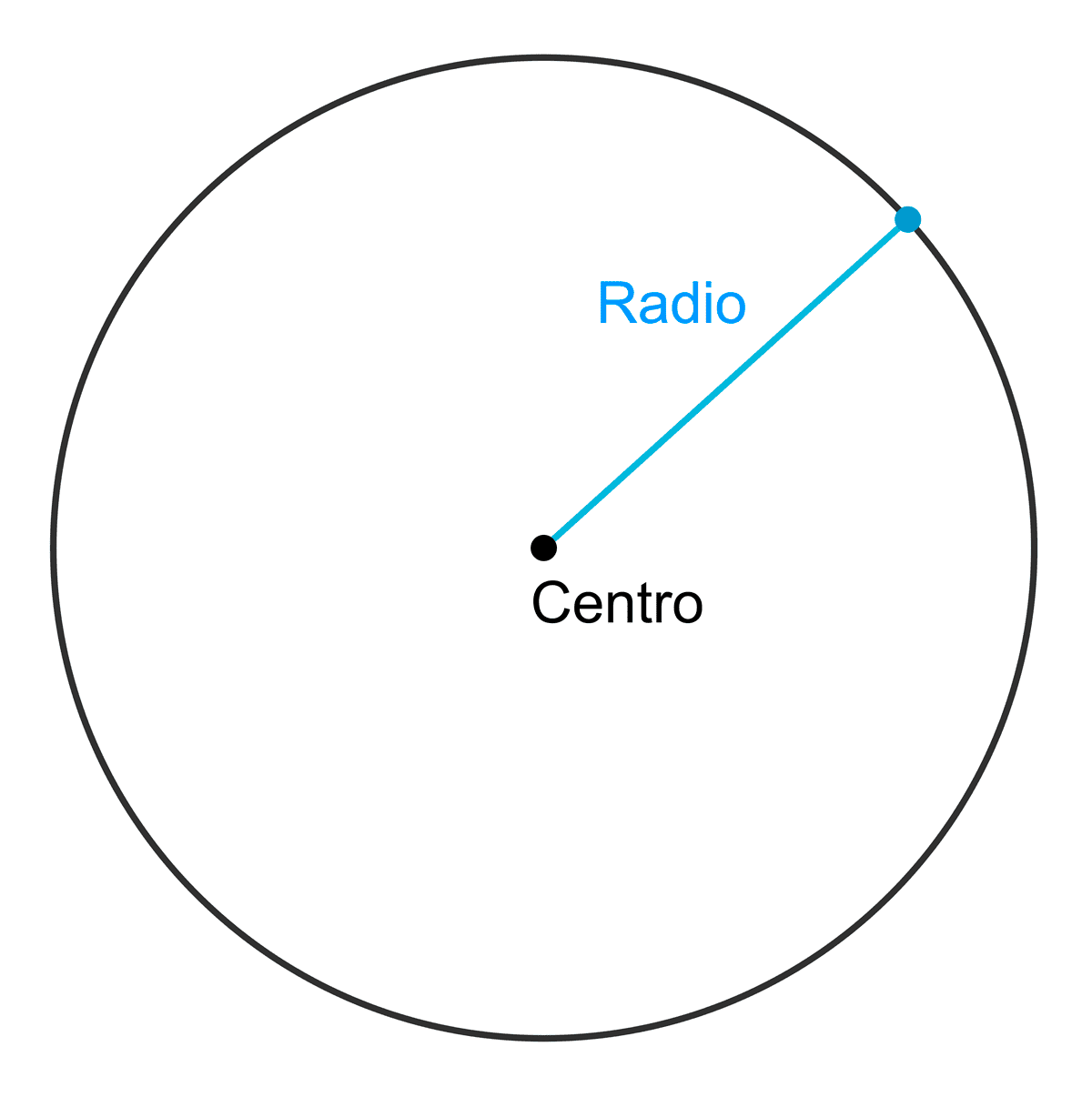
Radio
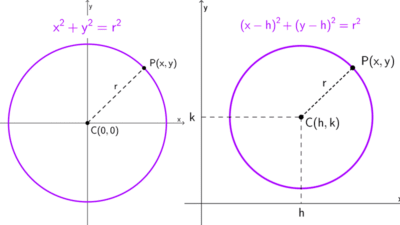
El radio es un segmento de recta que une el centro de la circunferencia con cualquier punto perteneciente a ella. Si el centro de la circunferencia es C(h, k) y un punto sobre ella es P(x, y), la longitud del radio r se calcula mediante la fórmula de la distancia:
\(r=\sqrt{(x-h)^2+(y-k)^2}\)
De hecho, la ecuación canónica de la circunferencia con centro (h, k) y radio r se deriva directamente de esta definición, elevando al cuadrado ambos miembros:
\((x-h)^2+(y-k)^2=r^2\)
Ejemplos
- La circunferencia \((x-2)^2+(y+3)^2=16\) tiene radio \(r=4\) ya que \(16=4^2.\)
- \((x-1)^2+(y+4)^2=5\) es la ecuación de una circunferencia con radio \(r=\sqrt{5}.\)
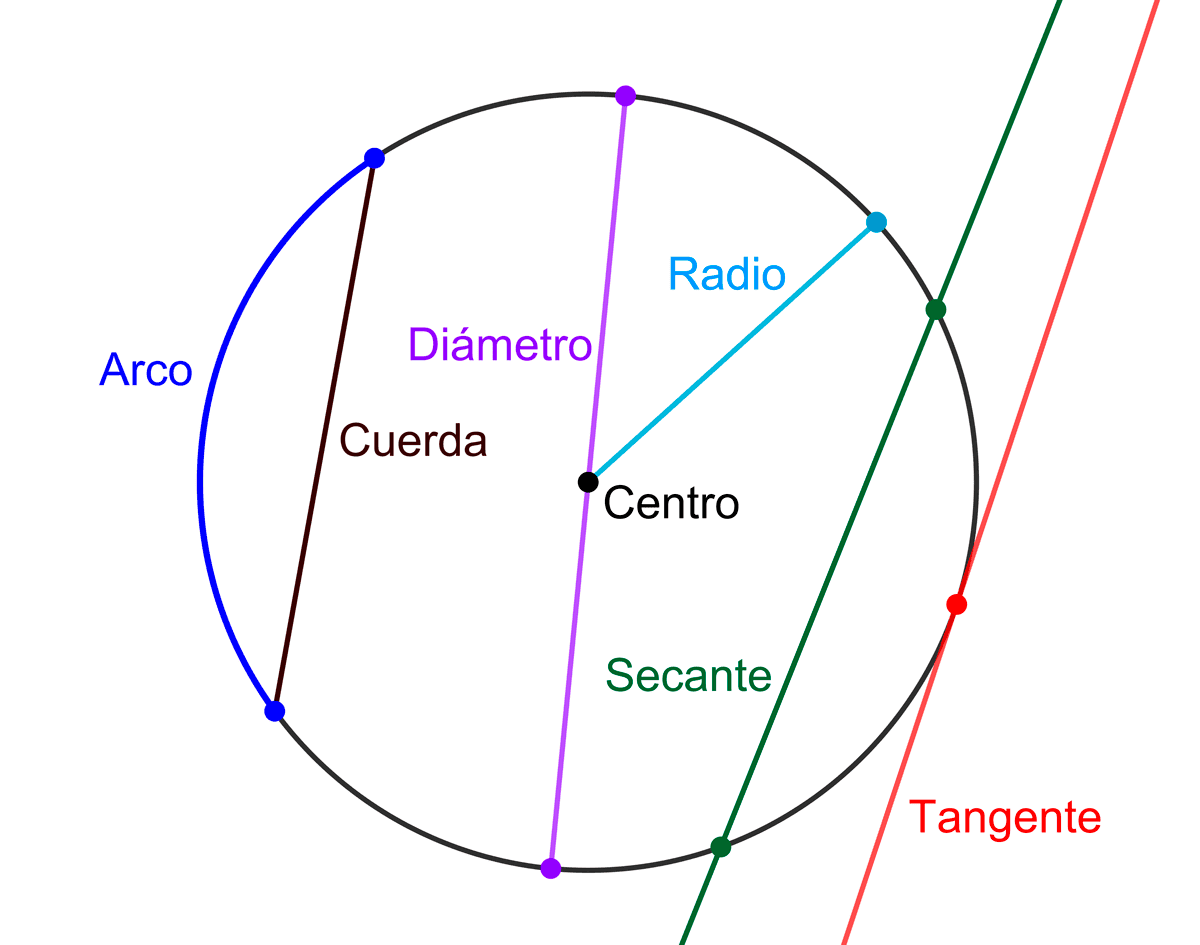
Diámetro
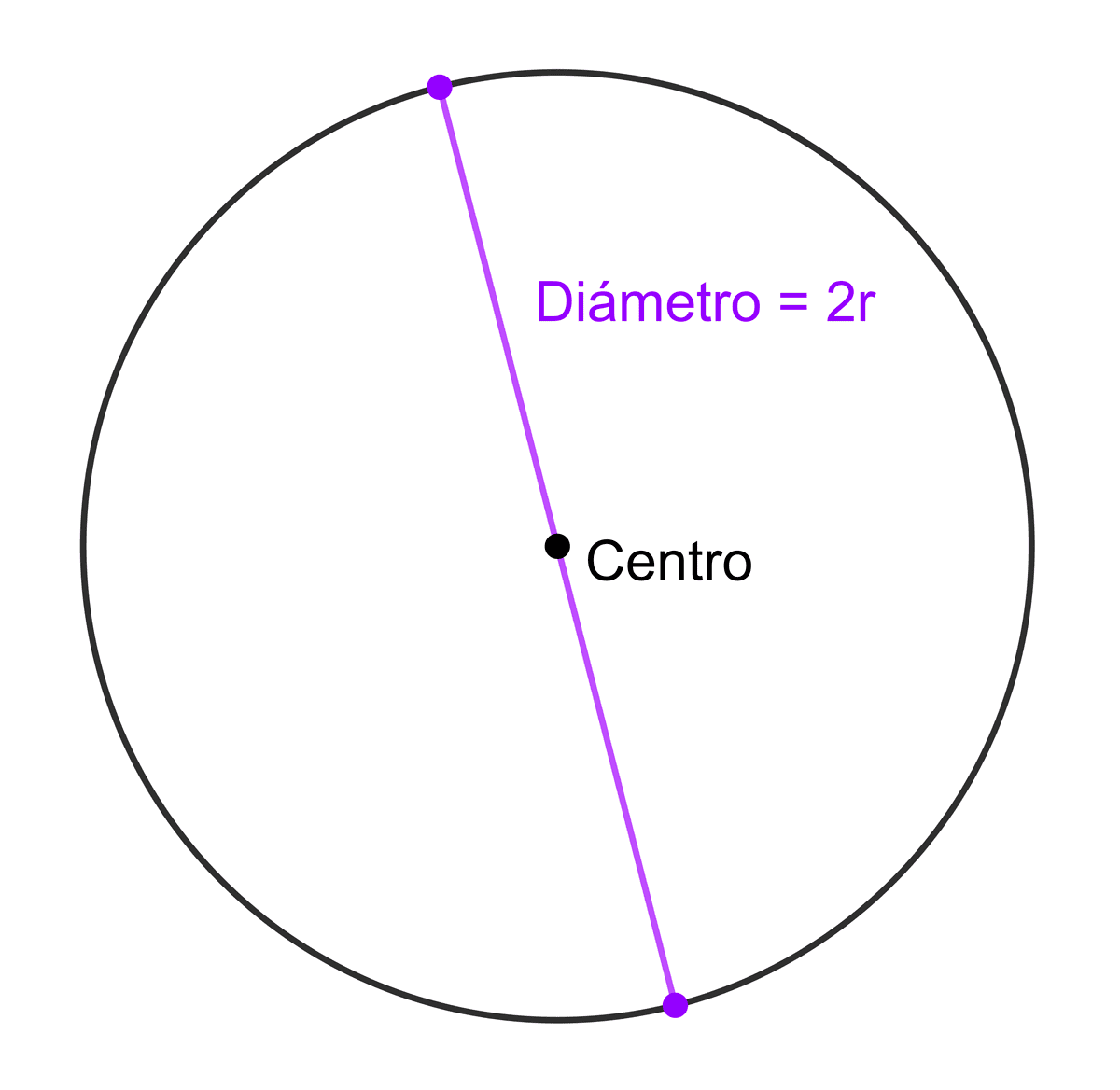
El diámetro es un segmento que une dos puntos de la circunferencia y pasa por el centro. Su longitud es el doble del radio:
\(d=2r\)
Cuerda
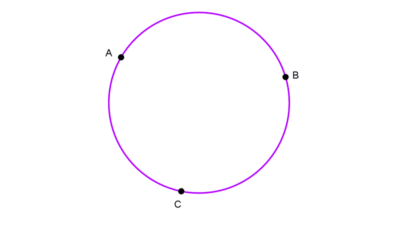
Una cuerda es un segmento de recta que une dos puntos cualesquiera de la circunferencia. A diferencia del diámetro, no es necesario que pase por el centro, aunque puede hacerlo. El diámetro es la cuerda de mayor longitud.
Dada una cuerda con extremos \(A(x_1, y_1)\) y \(B(x_2, y_2)\), su longitud se calcula como:
\(AB=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
Arco
Un arco es la porción de circunferencia comprendida entre dos puntos de la misma. Aunque no es un segmento, está directamente relacionado con las cuerdas, ya que cada cuerda determina dos arcos. En particular, si la cuerda es un diámetro, divide a la circunferencia en dos arcos iguales llamados semicircunferencias.
Flecha
La flecha (también llamada sagita) es el segmento que une el punto medio de un arco con el punto medio de su cuerda, y es perpendicular a la cuerda. Su longitud es la máxima distancia entre la cuerda y el arco que determina.
Recta secante
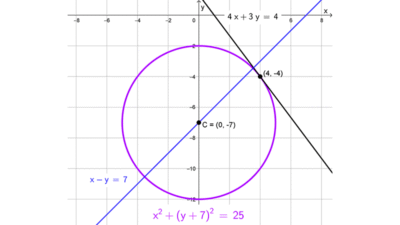
Una recta secante es aquella interseca a la circunferencia en dos puntos distintos. Analíticamente, las intersecciones de una recta y una circunferencia se encuentran resolviendo el sistema de ecuaciones formado por la ecuación de la recta y la ecuación de la circunferencia. Una recta será secante si este sistema tiene dos soluciones reales y distintas.
Recta tangente
Una recta tangente es aquella que interseca a la circunferencia en exactamente un punto, llamado punto de tangencia. Analíticamente, al resolver el sistema de ecuaciones entre la recta y la circunferencia, una recta será tangente si el sistema tiene una única solución real (una raíz doble).
Una propiedad fundamental de la tangente es que es perpendicular al radio en el punto de tangencia. Si el punto de tangencia es \((x_0, y_0)\) y el centro es \((h, k)\), la pendiente del radio es:
\(m_r=\dfrac{y_0-k}{x_0-h}\)
La pendiente de la recta tangente \(m_t\) será la opuesta y recíproca:
\(m_t=-\dfrac{1}{m_r}\), siempre que \(m_r \neq 0\)
Si \(m_r=0\) (radio horizontal), la tangente es vertical. Si \(m_r\) es indefinida (radio vertical), la tangente es horizontal. Conociendo el punto de tangencia y la pendiente, se puede determinar la ecuación de la recta tangente, la cual es:
\(y-y_0=m_t (x-x_0)\)
¿Te ha servido este contenido? ¡Califícalo!
Deja una respuesta

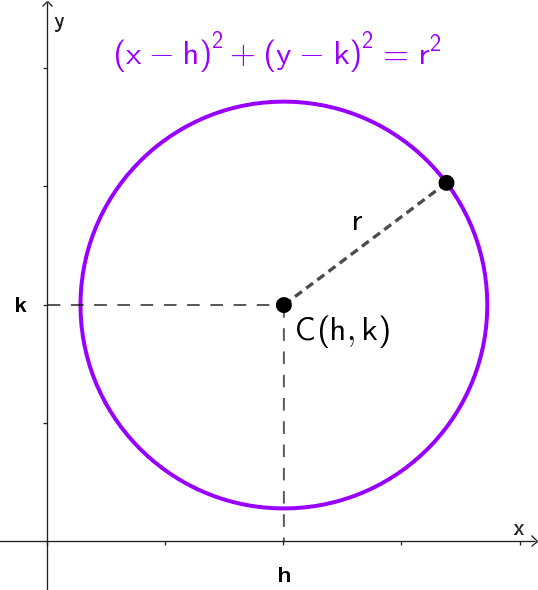







Otros artículos que pueden interesarte