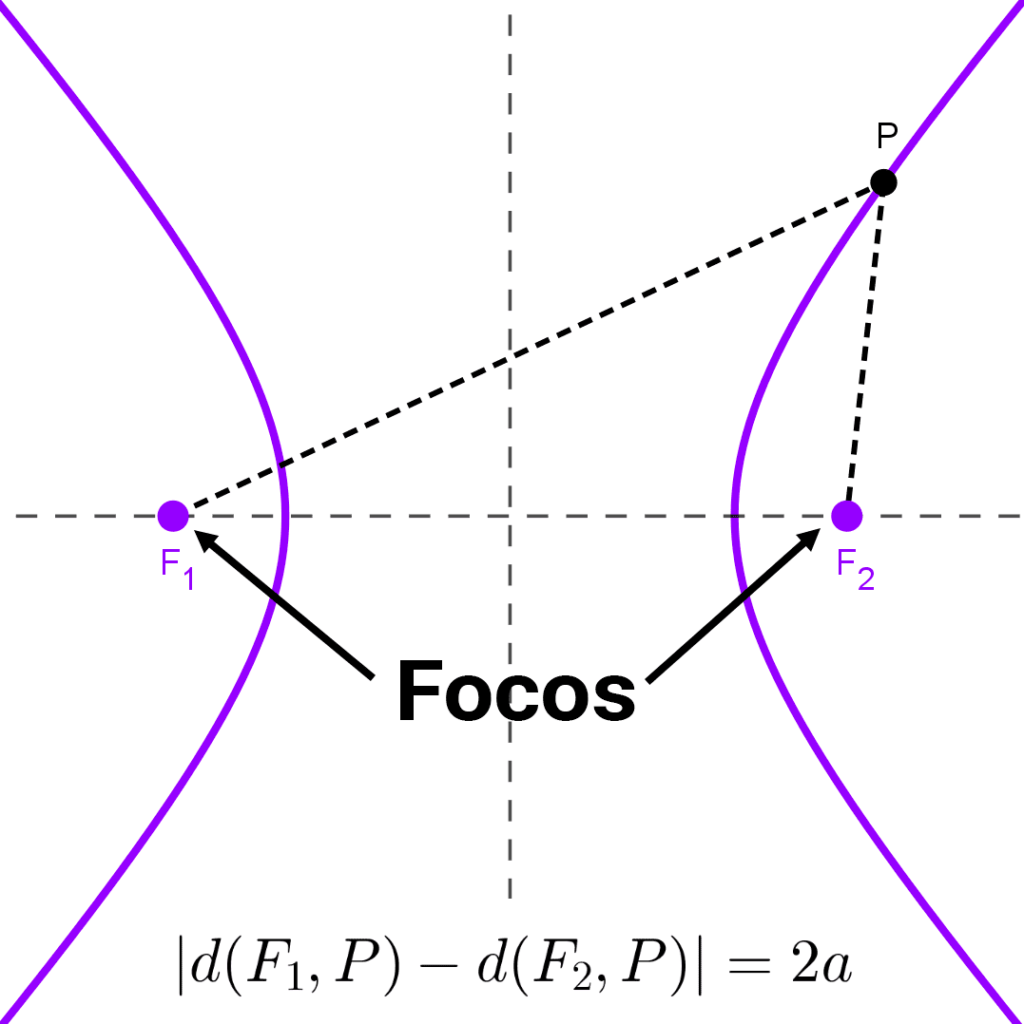
Focos de la hipérbola

En este artículo explicamos qué son y cómo determinar los focos de una hipérbola tanto si el centro es el origen u otro punto y si el eje transversal es horizontal o vertical. 

¿Qué son los focos?

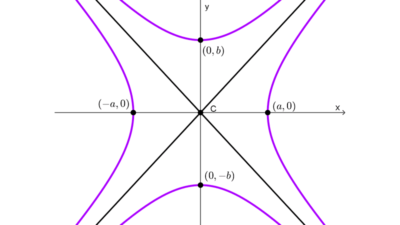
Los focos de la hipérbola son dos puntos fijos del plano que están sobre el eje focal, se encuentran separados por una distancia 2c denominada distancia focal. El punto medio entre los focos es el centro de la hipérbola. La característica principal de una hipérbola es que la diferencia en valor absoluto de distancias desde cualquier punto de la hipérbola hasta sus focos es una constante. 

¿Cómo hallar los focos?

Encontrar las coordenadas de los focos de la hipérbola es relativamente sencillo si se cuenta con la ecuación canónica. Es necesario reconocer si la hipérbola es horizontal (eje transversal sobre o paralelo al eje x) o vertical (eje transversal sobre o paralelo al eje y).

Esto último se determina a partir del término positivo en la ecuación canónica: si el término positivo contiene a la variable x, la hipérbola es horizontal; en cambio, si el término positivo es el que contiene a la variable y, la hipérbola es vertical. 

La distancia del centro a un foco se denomina semidistancia focal y está relacionada con los semiejes a través de la siguiente fórmula: *c=\sqrt{a^2+b^2}.* Recuerde que a² es el denominador del término positivo y b² es el denominador del término negativo en la ecuación canónica. Utilizaremos el valor de c para calcular los focos, como se muestra en la siguiente tabla:

Ecuación canónica	Eje transversal	Centro	Focos
*\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1*	Sobre el eje x	(0, 0)	(±c, 0)
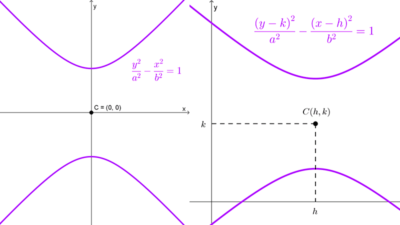
*\dfrac{y^2}{a^2}-\dfrac{x^2}{b^2}=1*	Sobre el eje y	(0, 0)	(0, ±c)
*\dfrac{(x-h)^2}{a^2}-\dfrac{(y-k)^2}{b^2}=1*	Paralelo al eje x	(h, k)	(h ± c, k)
*\dfrac{(y-k)^2}{a^2}-\dfrac{(x-h)^2}{b^2}=1*	Paralelo al eje y	(h, k)	(h, k ± c)

Ejercicios resueltos

A continuación, resolvemos algunos ejercicios sobre el cálculo de los focos en una hipérbola.

Ejercicio 1

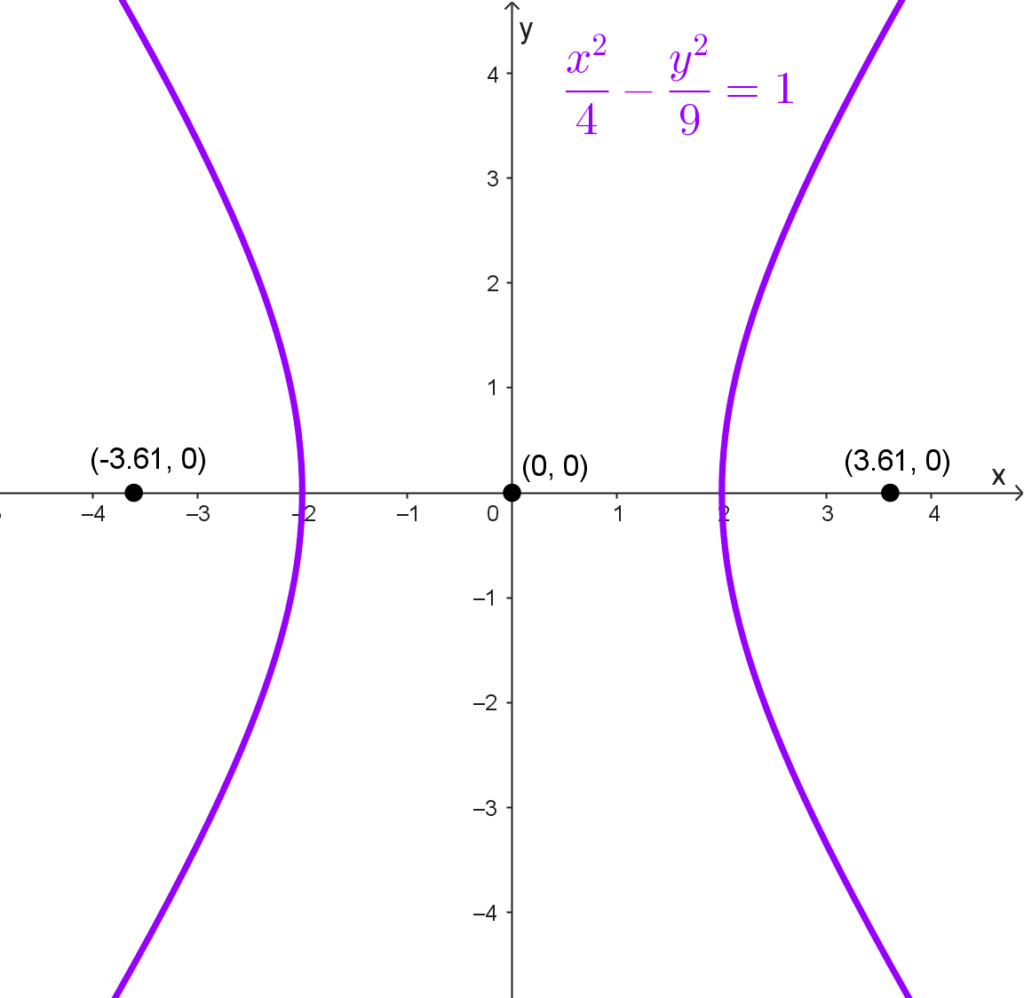
Obtener los focos de la hipérbola cuya ecuación es *\dfrac{x^2}{4}-\dfrac{y^2}{9}=1*

Solución: reconocemos mediante la ecuación canónica que el centro es el origen de coordenadas y que la hipérbola es horizontal, pues el término positivo contiene a la variable x. 

Según la fórmula de los focos de la hipérbola, estos se encuentran a c unidades del centro hacia la izquierda y la derecha. 

Para calcular el valor de c (semidistancia focal) primero extraemos los cuadrados de los semiejes que son denominadores en la ecuación:

*a^2=4*

*b^2=9*

Con estos datos podemos calcular c usando la relación fundamental:

*c=\sqrt{a^2+b^2}=\sqrt{4+9}=\sqrt{13}*

Como dijimos, los focos están a una distancia c del centro hacia la izquierda y la derecha:

*F_1(-c, 0)~~~ y~~~ F_2(c, 0)*

Sustituyendo *c=\sqrt{13}:*

*F_1(-\sqrt{13},0)~~~ y~~~ F_2(\sqrt{13},0)*

Usando aproximaciones: *F_1(-3,61; 0) ~~~y~~~ F_2(3,61 ;0)*

Ejercicio 2

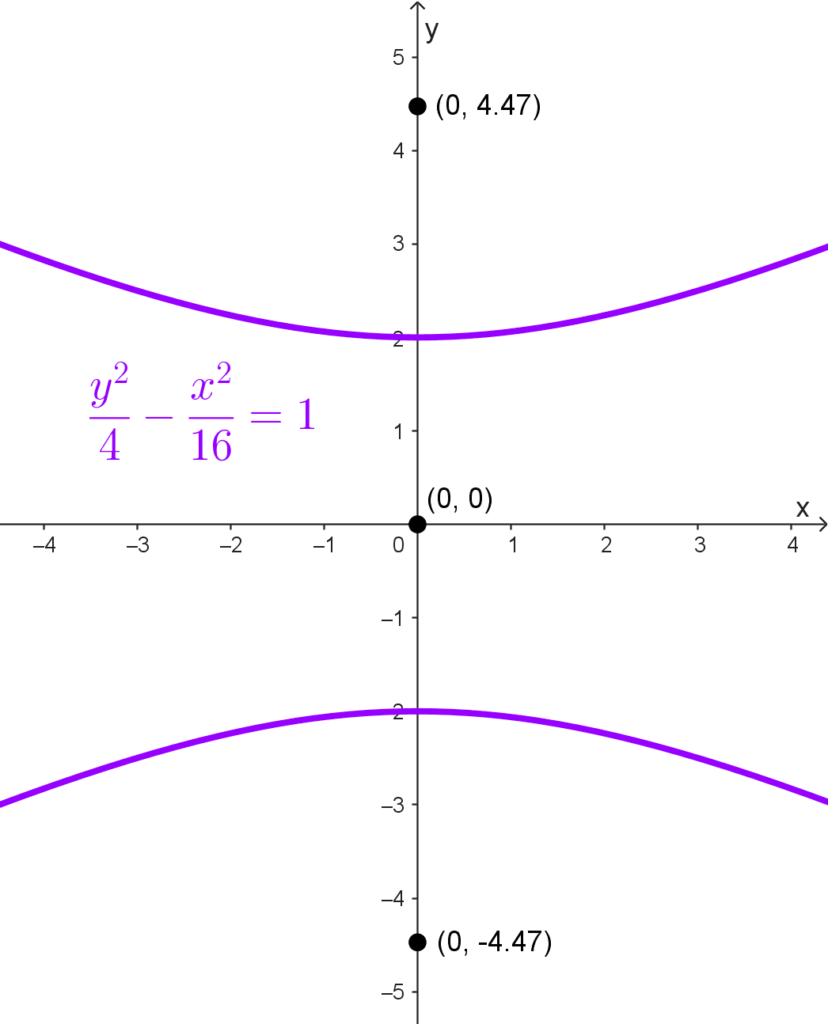
Sacar los focos de la hipérbola *\dfrac{y^2}{4}-\dfrac{x^2}{16}=1*

Solución: reconocemos que esta ecuación está en la forma canónica de una hipérbola vertical, ya que el término positivo está asociado a y². El centro de la hipérbola es el origen de coordenadas (0, 0).

Como primer paso, identificamos los valores de los cuadrados de los semiejes, que corresponden a los denominadores de la ecuación:

*a^2=4*

*b^2=16*

Luego, calculamos el valor de c, la semidistancia focal, utilizando la relación fundamental de las hipérbolas:

*c^2=a^2+b^2*

Sustituyendo los valores:

*c^2=4+16=20*

Por lo tanto:

*c=\sqrt{20}=2\sqrt{5}*

Llegamos al siguiente paso, que consiste en determinar las coordenadas de los focos. Para una hipérbola vertical, los focos se encuentran a una distancia c arriba y abajo del centro. Esto significa que las coordenadas serán:

*F_1(0, -c)~~ y~~ F_2(0, c)*

Sustituyendo *c=2\sqrt{5}:*

*F_1(0, -2\sqrt{5}) ~~~y~~~ F_2(0, 2\sqrt{5})*

Finalmente, realizamos una aproximación numérica:

*2\sqrt{5}≈4,47*

Esto nos da las coordenadas aproximadas de los focos:

*F_1(0; -4, 47) ~~~y~~~ F_2(0; 4, 47)*

Ejercicio 3

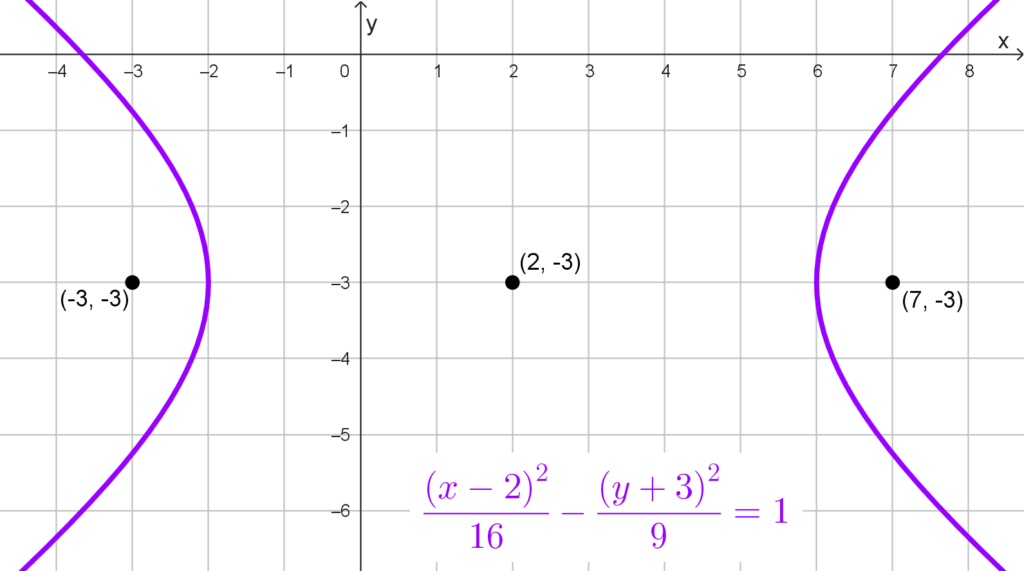
Hallar y graficar los focos de la hipérbola representada por la ecuación *\dfrac{(x-2)^2}{16}-\dfrac{(y+3)^2}{9}=1.*

Solución: reconocemos que esta ecuación está en la forma canónica de una hipérbola horizontal, ya que el término positivo está asociado a *(x-2)^2.* El centro de la hipérbola se encuentra en (h, k) = (2, -3).

Como primer paso, identificamos los valores de los cuadrados de los semiejes, que son los denominadores de la ecuación:

*a^2=16~~~ y~~~ b^2=9*

A continuación, calculamos el valor de la semidistancia focal utilizando la relación fundamental de las hipérbolas:

*c^2=a^2+b^2*

Sustituyendo los valores:

*c^2=16+9=25*

Por lo tanto:

*c=\sqrt{25}=5*

Para una hipérbola horizontal, los focos se encuentran a una distancia c hacia la izquierda y la derecha del centro. Esto significa que las coordenadas serán:

*F_1(h-c, k) ~~y~~ F_2(h+c, k)*

Sustituyendo los valores h = 2, k = -3 y c = 5:

*F_1(2-5, -3)=(-3, -3)~~~ y~~~ F_2(2+5, -3)=(7, -3)*

Ejercicio 4

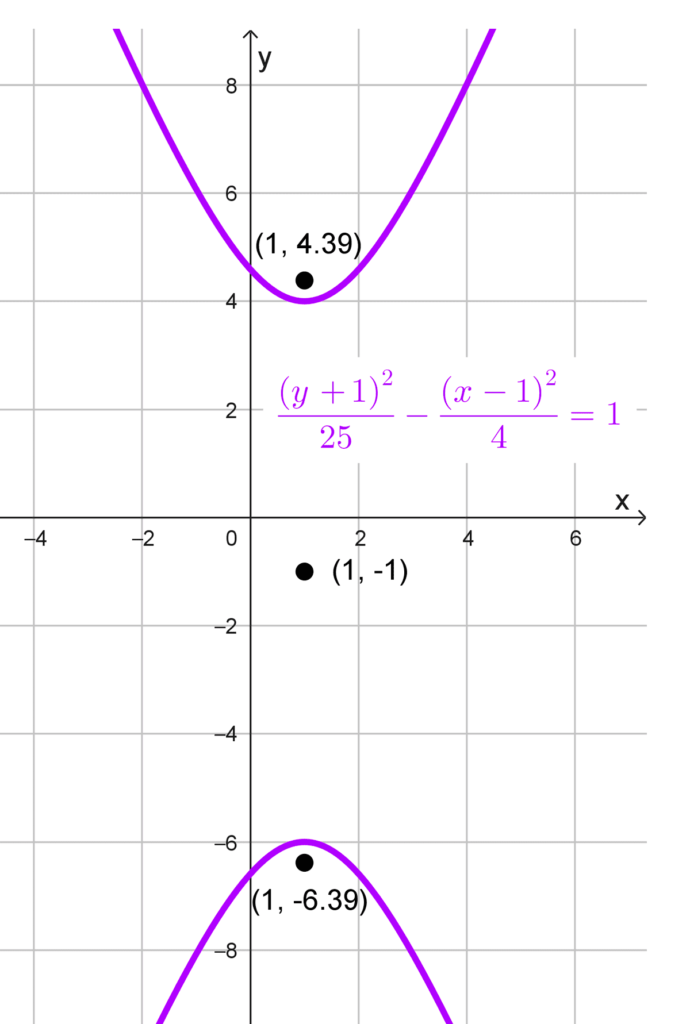
Determinar los focos de la hipérbola *\dfrac{(y+1)^2}{25}-\dfrac{(x-1)^2}{4}=1.*

Solución: observamos que esta ecuación corresponde a una hipérbola vertical, ya que el término positivo está asociado a *(y+1)^2.* El centro de la hipérbola se encuentra en (h, k) = (1, -1).

Identificamos los valores de los cuadrados de los semiejes, que están en los denominadores:

*a^2=25~~~ y~~~ b^2=4*

Para calcular c, utilizamos la relación característica de las hipérbolas:

*c^2=a^2+b^2*

Sustituyendo los valores correspondientes:

*c^2=25+4=29*

Por lo tanto:

*c=\sqrt{29}*

Ahora determinamos las coordenadas de los focos. Dado que se trata de una hipérbola vertical, los focos se encuentran a una distancia c hacia arriba y hacia abajo del centro. Esto implica que las coordenadas son:

*F_1(h, k-c)~~~ y~~~ F_2(h, k+c)*

Sustituyendo *h = 1, k = -1~~ y~~ c=\sqrt{29}:*

*F_1(1, -1-\sqrt{29}) ~~~y~~~ F_2(1, -1+\sqrt{29})*

Finalmente, hacemos una aproximación numérica, quedando:

*F_1(1; -6, 39)~~~ y~~~ F_2(1; 4, 39)*

Ejercicio 5

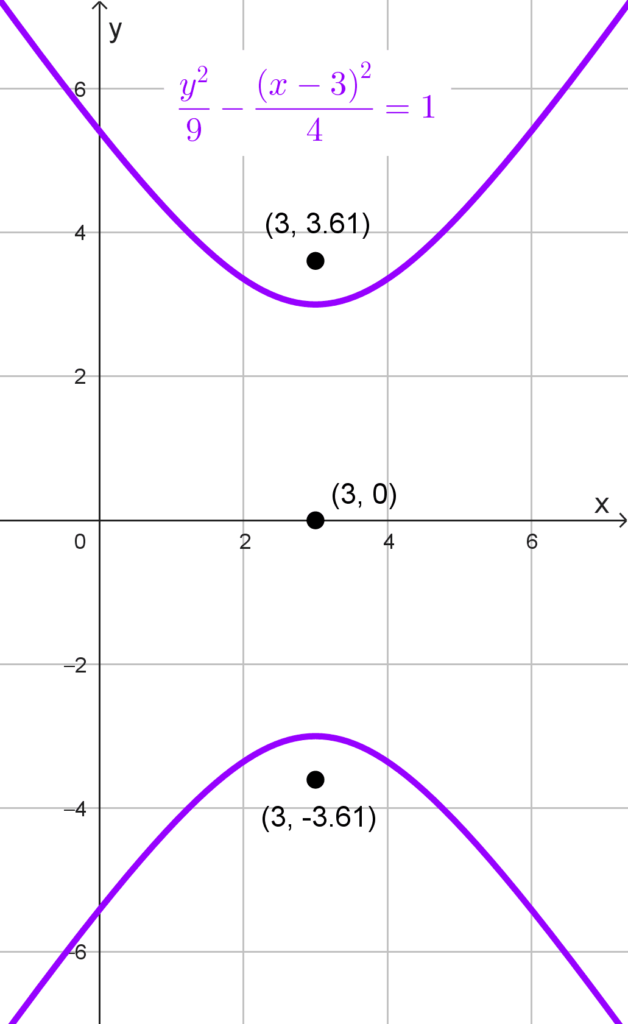
Encontrar los focos de *9x^2-4y^2-54x+117=0*

Solución: la ecuación no está en forma canónica así que no se puede usar directamente, sin embargo, si completamos los cuadrados obtendremos una forma equivalente:

*\dfrac{y^2}{9}-\dfrac{(x-3)^2}{4}=1*

Reconocemos que esta ecuación representa una hipérbola vertical, ya que el término positivo está asociado a y². El centro de la hipérbola está en (h, k) = (3, 0).

Identificamos los valores de los cuadrados de los semiejes, los cuales son los denominadores de la ecuación:

*a^2=9~~~ y~~~ b^2=4*

Calculamos la semidistancia focal empleando la relación fundamental de las hipérbolas:

*c^2=a^2+b^2*

Sustituyendo los valores:

*c^2=9+4=13*

Por lo tanto:

*c=\sqrt{13}*

Sabemos que, al tratarse de una hipérbola vertical, los focos están situados a una distancia c sobre y debajo del centro. Esto significa que las coordenadas de los focos son:

*F_1(h, k-c)~~~y~~~ F_2(h, k+c)*

Sustituimos *h=3, k=0 ~y~ c=\sqrt{13}:*

*F_1(3, 0-\sqrt{13})=F_1(3,-\sqrt{13})*

*F_2(3, 0+\sqrt{13})=F_2(3, \sqrt{13})*

Para obtener una aproximación numérica, calculamos que *\sqrt{13}≈3,61.* Entonces:

*F_1(3; -3, 61)~~ y~~ F_2(3; 3, 61)*

Ejercicio 6

Calcular los focos de la hipérbola de ecuación *3x^2-y^2-4y-40=0*

Solución: en este caso la ecuación está en forma general. Como en el anterior ejemplo completamos los cuadrados para obtener la expresión canónica: 

*\dfrac{x^2}{12}-\dfrac{(y+2)^2}{36}=1*

Esta ecuación corresponde a una hipérbola horizontal, ya que el término positivo está asociado a x². El centro de la hipérbola es (h, k) = (0, -2).

Identificamos los valores de los cuadrados de los semiejes a partir de los denominadores:

*a^2=12~~~ y~~~ b^2=36*

El siguiente paso es determinar el valor de c, la semidistancia focal, utilizando la fórmula:

*c^2=a^2+b^2*

Sustituyendo los valores:

*c^2=12+36=48*

Por lo tanto:

*c=\sqrt{48}=4\sqrt{3}*

Ahora determinamos las coordenadas de los focos. En una hipérbola horizontal, los focos se ubican a una distancia c hacia la izquierda y la derecha del centro. Las coordenadas quedan definidas como:

*F_1(h-c, k) ~~~y~~~ F_2(h+c, k)*

Sustituyendo *h=0, k=-2 ~y~ c=4\sqrt{3}:*

*F_1(0-4\sqrt{3}, -2)=F_1(-4\sqrt{3}, -2)*

*F_2(0+4\sqrt{3}, -2)=F_2(4\sqrt{3}, -2)*

Finalmente, hacemos una aproximación numérica, que nos da:

*F_1(-6, 93; -2)~~~y~~~ F_2(6, 93; -2)*