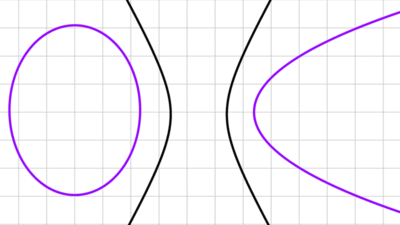
Invariantes de una cónica

En este artículo explicamos qué son los invariantes de una cónica y cómo se utilizan para determinar el tipo de cónica que representa una ecuación de segundo grado.

Invariantes 

Sabemos que, en geometría analítica, una cónica se representa mediante una ecuación de segundo grado con dos variables, cuya forma general es:

*Ax^2+Bxy+Cy^2+Dx+Ey+F=0*

donde A, B, C, D, E, y F son coeficientes reales que determinan la forma y la orientación de la cónica en el plano. Cuando se aplican transformaciones como rotaciones o traslaciones al sistema de coordenadas, la ecuación de la cónica adopta una nueva forma, con coeficientes modificados que reflejan estos cambios en el plano. La ecuación transformada se puede expresar como:

*A'x'^2+B'x'y'+C'y'^2+D'x'+E'y'+F'=0*

donde A', B', C', D', E' y F' son los nuevos coeficientes resultantes de la transformación aplicada. 

A pesar de estos cambios en la ecuación, ciertas cantidades, conocidas como invariantes, permanecen constantes. Los tres invariantes asociados a una cónica son el discriminante, el determinante de la matriz asociada y la suma de los coeficientes principales. Sus fórmulas son las siguientes:

1. Discriminante: Δ = B² - 4AC
2. Determinante de la matriz asociada:  *δ=\begin{vmatrix} 2A & B & D \\ B & 2C & E \\ D & E & 2F \\ \end{vmatrix}*
3. Suma de los coeficientes principales: ω = A + C

Es posible utilizar estas cantidades para caracterizar una ecuación (determinar a qué cónica corresponde). El discriminante, Δ = B² - 4AC, es fundamental para determinar el tipo de cónica representada por la ecuación. Según el valor de Δ, podemos identificar si la curva es una circunferencia o elipse (cuando Δ < 0), una parábola (cuando Δ = 0), o una hipérbola (cuando Δ > 0).

El determinante de la matriz asociada, δ, nos indica si la ecuación corresponde a una cónica regular o degenerada. Si δ ≠ 0, la cónica es regular. Si δ = 0, la cónica es degenerada, lo que significa que representa una figura reducida como un punto o un par de líneas rectas.

Al identificar una elipse es importante considerar el valor de tercer invariante. Cuando el determinante δ ≠ 0 y el discriminante Δ < 0, la ecuación puede representar una elipse real o un conjunto vacío (elipse imaginaria). Para saber cuál es el caso, se debe analizar la relación entre el signo de δ y el de A+C.

Si ocurre que signo(δ) = signo(A + C), la ecuación representa un conjunto vacío, como en el caso de la ecuación x² + y² = -1, que no tiene puntos reales en el plano. En cambio, si signo(δ) ≠ signo(A+C), la ecuación describe una elipse real, es decir, un conjunto no vacío de puntos. Cuando δ = 0 y Δ < 0, la elipse se degenera en un solo punto. 

Clasificación de ecuaciones mediante invariantes

El proceso de caracterizar la ecuación de una cónica utilizando invariantes es conocido como el método de invariantes. En la siguiente tabla se resumen los casos posibles.

Determinante δ	Discriminante Δ	Cónica
δ ≠ 0	B2 - 4AC < 0	Elipse real si signo (δ) ≠ signo (A+C). Elipse imaginaria si signo (δ) = signo (A+C)
δ = 0	B2 - 4AC < 0	Elipse degenerada: un punto real.
δ ≠ 0	B2 - 4AC > 0	Hipérbola real
δ = 0	B2 - 4AC > 0	Hipérbola degenerada: dos líneas rectas que se cortan.
δ ≠ 0	B2 - 4AC = 0	Parábola real
δ = 0	B2 - 4AC = 0	Parábola degenerada: par de rectas paralelas o superpuestas, reales o imaginarias.

Ejemplos

Ejemplo 1

Analizar la ecuación *x^2-2xy+y^2+3x=0*

Solución: identificamos los coeficientes en la forma general de la ecuación de segundo grado *Ax^2+Bxy+Cy^2+Dx+Ey+F=0,* donde en este caso tenemos: A=1, B=-2, C=1, D=3, E=0, y F=0.

El primer paso es calcular el determinante de la matriz asociada a esta cónica:

*\delta=\begin{vmatrix} 2A & B & D \\ B & 2C & E \\ D & E & 2F \end{vmatrix} =\begin{vmatrix} 2(1) & -2 & 3 \\ -2 & 2(1) & 0 \\ 3 & 0 & 2(0) \end{vmatrix}*

Desarrollamos el determinante:

*\delta=(2)(2)(0)-(2)(1)(0)^2-(2)(-2)^2(0)+2(-2)(0)(3)-2(1)(3)^2*

Simplificando esta expresión, obtenemos:

*\delta=0-0-0+0-18=-18*

El resultado es δ = -18, un valor distinto de cero, lo cual indica que la cónica es regular. Para clasificar más específicamente esta cónica, evaluamos el discriminante:

*\Delta=B^2-4AC=(-2)^2-4(1)(1)=4-4=0*

El discriminante Δ = 0 indica que la cónica es una parábola en el plano cartesiano.

Ejemplo 2

Analizar la ecuación *2x^2-xy-y^2+2x+y=0*

Solución: primero, identificamos los coeficientes de la ecuación en la forma general, ellos son A=2, B=-1, C=-1, D=2, E=1, y F=0.

Calculamos el determinante de la matriz asociada a la ecuación cuadrática:

*\delta= \begin{vmatrix}  2A & B & D \\  B & 2C & E \\  D & E & 2F \end{vmatrix}=\begin{vmatrix} 2(2) & -1 & 2 \\ -1 & 2(-1) & 1 \\ 2 & 1 & 2(0) \end{vmatrix}*

Desarrollamos el determinante:

*\delta=8\cdot(-2)\cdot0-2\cdot2\cdot1^2-2\cdot(-1)^2\cdot0+2\cdot(-1)\cdot1\cdot2-2\cdot(-1)\cdot2^2*

Simplificando, obtenemos:

*\delta=0-4-0-4+8=0*

El resultado es δ = 0, lo que indica que la cónica es degenerada. Ahora, para clasificar el tipo de degeneración, calculamos el discriminante:

*\Delta=B^2-4AC=(-1)^2-4(2)(-1)=1+8=9*

El valor del discriminante es Δ = 9, que es mayor que cero. Esto indica que la cónica es una hipérbola degenerada, lo cual se manifiesta como un par de líneas reales que se intersectan. 

Este ejemplo ha sido extraído del artículo de cónicas degeneradas, donde podrás encontrar más ejemplos de estos casos:

Cónicas degeneradas: explicación y ejemplos

Ejemplo 3

Analizar la ecuación *y^2-8xy+17x^2+4=0*

Solución: identificamos los coeficientes que corresponden a la forma general de una cónica, encontrando: A=17, B=-8, C=1, D=0, E=0, y F=4.

Primero, calculamos el determinante de la matriz asociada para verificar la naturaleza de la cónica:

*\delta=\begin{vmatrix} 2A & B & D \\ B & 2C & E \\ D & E & 2F \end{vmatrix} =\begin{vmatrix} 2(17) & -8 & 0 \\ -8 & 2(1) & 0 \\ 0 & 0 & 2(4) \end{vmatrix}*

Desarrollando este determinante, tenemos:

*\delta=(34)(2)(8)-2(17)(0)^2-2(-8)^2(4)+2(-8)(0)(0)-2(1)(0)^2*

Simplificando:

*\delta=34\cdot2\cdot8-0-2\cdot64\cdot4+0-0=544-512=32*

El determinante es δ = 32, un valor distinto de cero, lo que confirma que la cónica es regular. Para precisar de qué tipo de cónica se trata, evaluamos el discriminante:

*\Delta=B^2-4AC=(-8)^2-4(17)(1)=64-68=-4*

El discriminante Δ = -4, al ser negativo, indica que la cónica es una elipse. Ahora bien, podría ser una elipse real o imaginaria, para determinarlo analizamos el tercer invariante: 

*A + C = 17+1=18*

Como los signos de A+C y de δ son ambos positivos: signo (δ) = signo (A+C), resulta que la ecuación representa a una elipse imaginaria, es decir, no hay puntos reales que cumplan la ecuación.