Lado recto de una elipse
En este artículo explicamos qué es y cómo calcular el lado recto de una elipse con ejercicios resueltos paso a paso. Además, veremos una demostración de la fórmula del lado recto.
Índice
¿Qué es el lado recto?
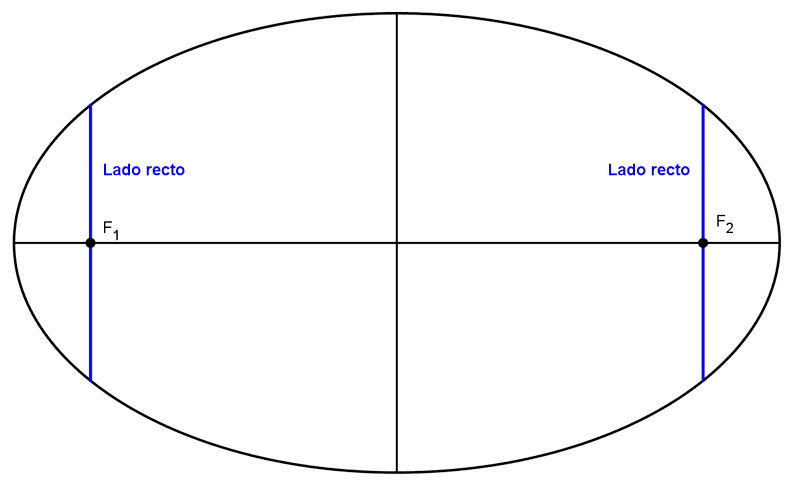
El lado recto de una elipse es un segmento que une dos puntos de la misma, es perpendicular al eje mayor y pasa por un foco. Una elipse tiene dos lados rectos, uno por cada foco, y sus longitudes pueden obtenerse con la siguiente fórmula:
*L_R= \dfrac{2b^2}{a}*
Ejercicios resueltos
A continuación veremos algunos ejemplos del cálculo del lado recto de elipses.
Ejercicio 1
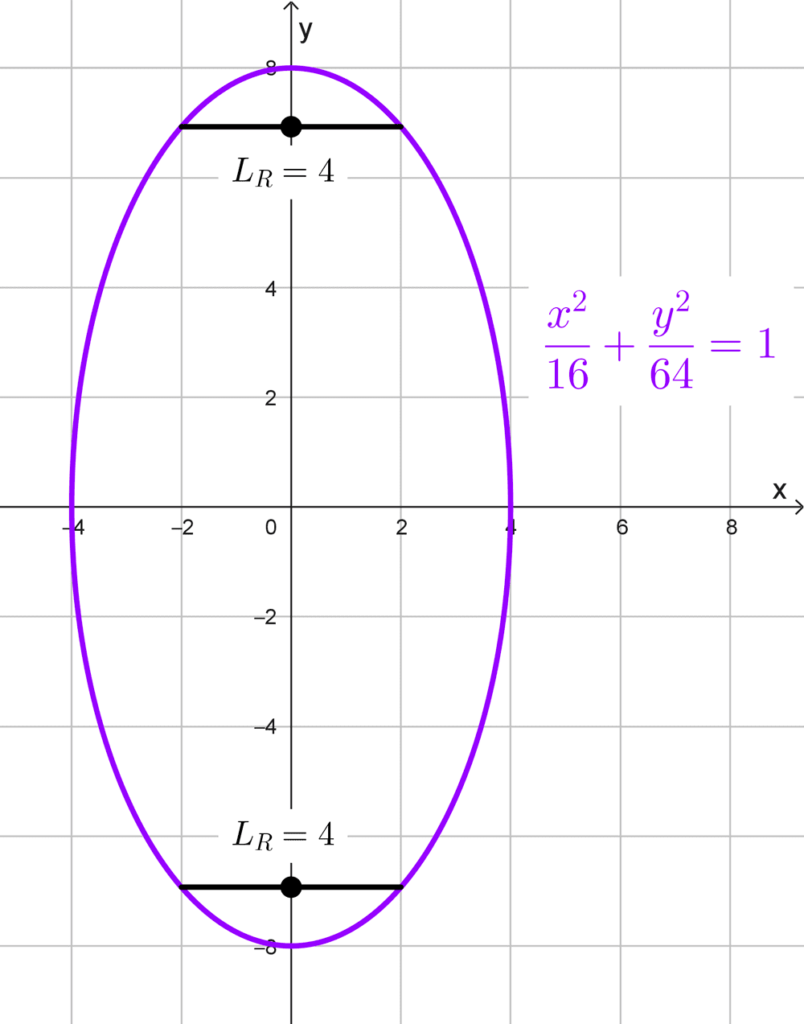
Obtener el lado recto de la elipse *\dfrac{x^2}{16}+\dfrac{y^2}{64}=1*
Solución: la ecuación está en forma canónica así que podemos extraer los datos que necesitamos:
*a^2=64 → a=\sqrt{64}=8*
*b^2=16*
Para determinar la longitud del lado recto, reemplazamos los datos en la fórmula:
*L_R=\dfrac{2b^2}{a}*
*=\dfrac{2\cdot 16}{8}*
*=\dfrac{32}{8}*
*=4*
Para poder graficar el lado recto primero se debe conocer la ubicación de los focos, puedes aprender cómo hacerlo en este artículo:
Ejercicio 2
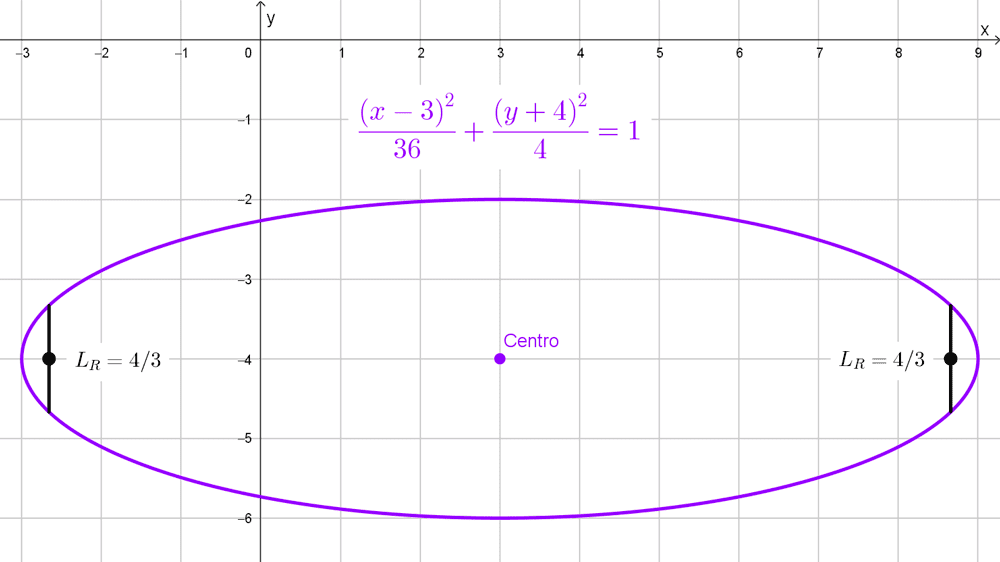
Calcular la longitud del lado recto de la elipse con ecuación *\dfrac{(x-3)^2}{36}+\dfrac{(y+4)^2}{4}=1*
Solución: de la ecuación podemos leer que la elipse no está centrada en el origen como en el caso anterior, sin embargo, este hecho no afecta la longitud del lado recto. Extraemos los datos necesarios:
*a^2=36→a=\sqrt{36}=6*
*b^2=4*
Con estos valores sacamos el lado recto:
*L_R=\dfrac{2b^2}{a}*
*=\dfrac{2\cdot 4}{6}*
*=\dfrac{8}{6}*
*=\dfrac{4}{3}*
*=1,33…*
Ejercicio 3
Hallar el valor del lado recto de la elipse *2x^2+4x+7y^2-28y-40=0*
Solución: en este caso, tenemos la ecuación general y no la canónica, por tanto no podemos extraer directamente los datos necesarios. Si realizamos el proceso de completar los cuadrados, llegaremos a la siguiente ecuación:
*\dfrac{(x+1)^2}{35}+\dfrac{(y-2)^2}{10}=1*
Con la ecuación en esta forma sí podemos sacar los datos necesarios:
*a^2=35 → a=\sqrt{35}*
*b^2=10*
Entonces:
*L_R=\dfrac{2b^2}{a}*
*=\dfrac{2\cdot 10}{\sqrt{35}}*
*=\dfrac{20}{\sqrt{35}}*
*≈3,38*
Demostración
Vamos a demostrar que el lado recto de una elipse tiene longitud *L_R=\dfrac{2b^2}{a}.*
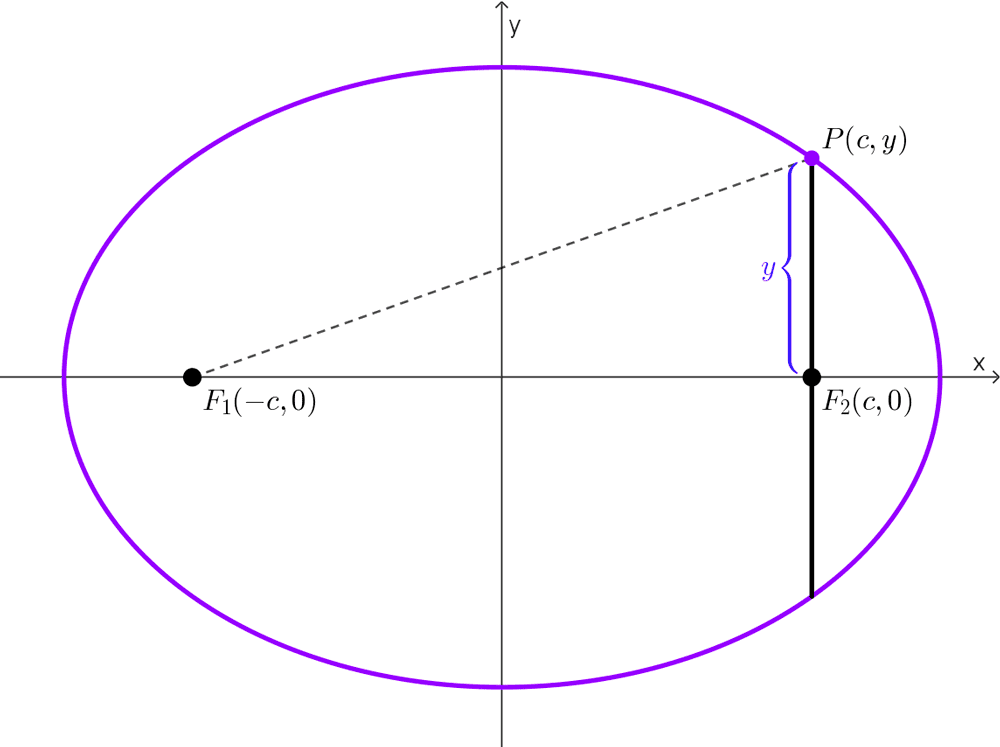
Comenzamos con una elipse ubicada de forma conveniente en el plano cartesiano como se muestra en el gráfico. Consideremos uno de los extremos del lado recto, por ejemplo, P (c, y).
Por definición de elipse, debe cumplirse que:
*d(F_1, P)+d(F_2,P)=2a*
*\sqrt{(c-(-c))^2+(y-0)^2}+\sqrt{(c-c)^2+y^2}=2a*
*\sqrt{(2c)^2+y^2}+\sqrt{y^2}=2a*
Si consideramos y > 0, entonces:
*\sqrt{(2c)^2+y^2}+y=2a*
*\sqrt{4c^2+y^2}=2a-y*
*(\sqrt{4c^2+y^2})^2=(2a-y)^2*
*4c^2+y^2=4a^2-4ay+y^2*
*4c^2+\cancel{y^2}=4a^2-4ay+\cancel{y^2}*
*4ay=4a^2-4c^2*
*4ay=4(a^2-c^2)*
*y=\dfrac{a^2-c^2}{a}*
Debido a que *a^2-c^2=b^2,* se concluye que:
*y=\dfrac{b^2}{a}*
Como la ordenada del punto P corresponde a la mitad del lado recto, se tiene que la longitud del lado recto es:
*L_R=2\dfrac{b^2}{a}*
Como se quería demostrar.
Recursos adicionales
Los siguientes videos explican el lado recto de una elipse:
Última actualización del contenido: 01/11/2024
Deja una respuesta




Otros artículos que pueden interesarte